Вычисление интегралов
Продолжим изучение данного "каверзного" интеграла. Опробуем силы Maple 7 на интеграле более общего вида, где конкретный показатель степени заменен на обобщенный -n. Здесь нас ожидает приятный сюрприз – Maple 7 с легкостью выдает аналитическое решение для данного определенного интеграла:
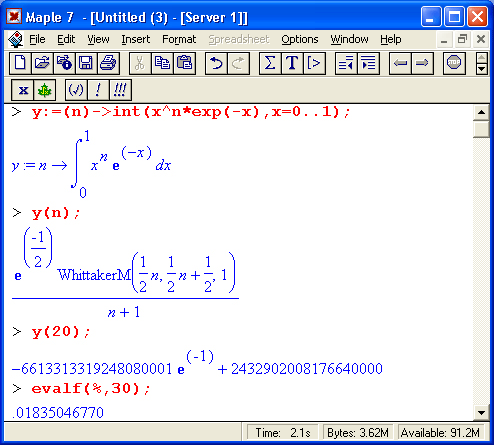
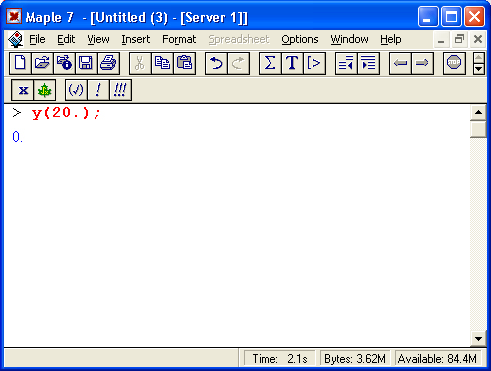
Однако радоваться несколько преждевременно. Многие ли математики знают, что это за специальная функция – WhittakerM? Студенты, любящие подшучивать над своим профессором, могут попробовать спросить у него об этом. Скорее всего, профессор стушуется, а потом будет долго копаться в литературе, прежде чем найдет ее определение и сможет разъяснить, что это такое. Но хуже другое – Maple 7 при конкретном n = 20 дает грубо неверное решение – 0 (почему – уже объяснялось). Забавно, что при этом сама по себе функция WhittakerM вычисляется для n = 20 без проблем:
> WhittakerM(10.10.5.1); 6353509348
А теперь присмотритесь к новому результату вычисления злополучного интеграла. Оказывается, он уже не содержит больших чисел, свойственных прямому решению! Зная значение WhittakerM с погрешностью по умолчанию, можно уверенно вычислить приближенное численное значение интеграла с той же погрешностью, уже не прибегая к арифметике высокой точности:
> (exp(-0.5)*WihittakerM(10.10.5.1))/21; 01835046770
