Вычисление интегралов
Возьмем еще один наглядный пример – вычисление интеграла от синусоидальной функции при произвольно больших пределах, но кратных 2π! Очевидно, что при этом (учитывая равность площадей положительной и отрицательной полуволн синусоиды) значение интеграла будет равно 0. Например:
> int(sin(x),x-1000*pi..l000*pi); 0
Однако распространение этого правила на бесконечные пределы интегрирования является грубейшей ошибкой. Интеграл такого рода уже не берется (или говорят, что он не сходится), и Maple 7 дает соответствующий результат:
> int(sin(x),x=-infinity..infinity); undefined
Во многих областях техники часто употребляются выражения "затухающая синусоида" или "нарастающая синусоида". Иногда говорят и о "синусоиде с уменьшающейся или возрастающей амплитудой". Бесполезно утверждать, что эти названия принципиально ошибочны – в рамках допущений, принятых в технических расчетах, такие утверждения весьма наглядны и эта, в частных случаях вполне оправданная, наглядность с позиций математики идет в ущерб точности фундаментальных определений.
Возьмем, к примеру, широко распространенную функцию: y(t) = exp(-t)sin(2*Pi*t). Построим ее график и вычислим определенный интеграл от этой функции с пределами от 0 до ∞ (рис. 8.4).
С первого взгляда на график видно, что каждая положительная полуволна функции (затухающей "синусоиды") явно больше последующей отрицательной полуволны. К тому же осцилляции функции быстро затухают и через десяток-другой периодов значение функции становится исчезающе малым. Вот почему Maple 7 уверенно вычисляет интеграл с такой подынтегральной функцией. Ее свойство – неопределенность при t › ∞ исчезает.
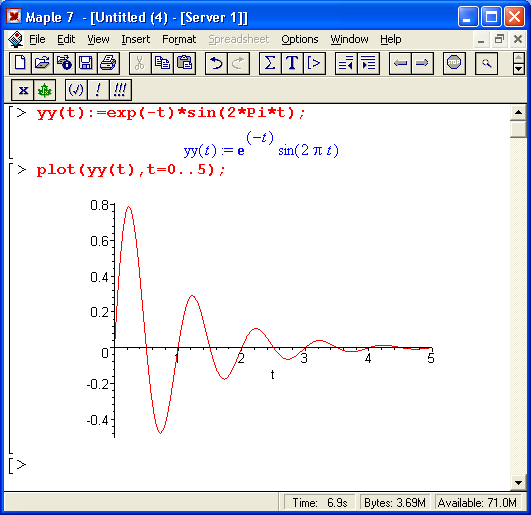
Рис. 8.4. График "затухающей синусоиды" и интеграл от нее с пределами от 0 до бесконечности
Однако называть такую функцию "затухающей синусоидой", безусловно, неточно. Умножение sin(2pt) на множитель, зависящий от времени t, лишает функцию главного свойства синусоиды – ее строгой симметрии. Так что exp(-t)sin(2pt) – это совсем новая функция со своими отличительными свойствами. Главные из них – несимметрия при малых t и исчезающе малые значения при больших t. Ни тем, ни другим свойством обычная синусоида не обладает. А теперь возьмем антипод этой функции – "синусоиду с экспоненциально нарастающей до стационарного значения 1 амплитудой".
Такая функция записывается следующим образом:
Y(t) = (1 -exp(-t)) sin(2*Pi*t).
Ее график и попытки вычисления интеграла с такой подынтегральной функцией приведены на рис. 8.5.
