Нахождение функции Лагранжа системы и частоты малых колебаний
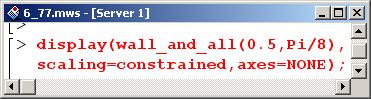
Теперь можно отобразить всю систему. Координату центральной точки бруска примем равной 0.5, а угол отклонения стержня – π/8.
Внимание!
Процедурой wall_and_all() картинка формируется, но не отображается! Для ее отображения следует использовать процедуру display() из пакета plots.
На заметку
Если выделить рисунок и из раскрывающегося меню выбрать подменю Axes (Оси), а затем одну из команд выбора системы координат (любая, кроме None (Отсутствуют): Boxed (В рамке), Frame (Точка пересечения в левом углу) или Normal (Обычные)), на рисунке будут отображены координатные оси. В этом случае несложно заметить, что центральная точка бруска расположена несколько правее метки 0.5. Дело в том, что координата центральной точки бруска равна 0.5 до переноса картинки на (1-Sft) вверх и Sft/N вправо. После переноса вправо координата центральной точки равна 0.5+Sft/N.
Далее приступаем непосредственно к решению задачи. Но прежде следует "сбросить" значение, присвоенное переменной 1. Эта переменная используется непосредственно в решении, а решение необходимо получить в символьном виде. Поэтому выполняем следующую команду.
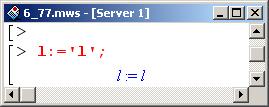
Для определения функции Лагранжа нужно задать кинетическую и потенциальную энергии системы. Кинетической энергией обладают движущийся брусок и совершающий колебания шарик (стержень и пружину считаем невесомыми, поэтому кинетической энергией они не обладают).
Кинетическая энергия Т1 () бруска равна половинному произведению массы бруска М на его скорость v. Определяем данную зависимость ка функцию от скорости.
Кинетическая энергия шарика определяется не так просто, поскольку закон его движения есть суперпозиция движения центра бруска и непосредственно шарика относительно бруска – ведь колебания шарик совершает относительно бруска, а относительно неподвижной системы координат движения шарика намного сложнее. В общем случае кинетическая энергия шарика Т2 зависит от трех параметров: скорости бруска v, угловой скорости шарика omega в системе координат, связанной с бруском, и угла phi отклонения стержня относительно вертикали.
На заметку
Относительная линейная скорость колебательных движений шарика равна произведению угловой скорости шарика на длину стержня и направлена по касательной к описываемой шари ком траектории, т.е. перпендикулярно стержню. Из элементарных геометрических соображений очевидно, что проекция этой скорости на горизонтальную ось дается умножением на косинус угла отклонения стержня от вертикали, а на вертикальную – умножением на синус. Чтоб1 найти абсолютную скорость шарика, нужно сложить соответствующие проекции скорости бру ска и относительной скорости шарика на горизонталь и вертикаль. Поскольку брусок движете вдоль горизонтали, проекция его скорости на горизонталь совпадает с этой скоростью, а вертикальная проекция равна нулю. В выражении для кинетической энергии используется квадрат абсолютной скорости. Как известно, квадрат вектора равен сумме квадратов его проекции на перпендикулярные оси. Этим свойством и воспользуемся ниже.
Таким образом, кинетическая энергия шарика определяется как функция трех параметров.
