Нахождение функции Лагранжа системы и частоты малых колебаний
Из последнего уравнения, как нетрудно заметить, можно выразить и отклонения. Сделаем это (команда solve(Eq2new,phi(t))), и полученное выражение для функции phi(t) подставим в первое уравнение.

Упрощаем результат.
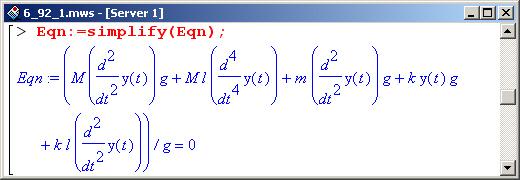
Составим характеристическое уравнение. Поэтому в уравнении Eqn выполняем соответствующую замену, после чего уравнение сокращаем на экспоненту (еще умножаем на g) и упрощаем.

Полученное уравнение определяет частоты собственных колебаний системы. Эти частоты (точнее, частоты в квадрате) можно найти.

Чтобы нагляднее представить, как выглядит система "в действии", создадим анимационную картинку. Но прежде присвоим параметрам, используемым в задаче, конкретные значения.

