Нахождение функции Лагранжа системы и частоты малых колебаний
Кинетическая энергия системы Т() равна сумме кинетических энергий бруска и шарика и также является функцией трех параметров: скорости бруска v, угловой скорости шарика omega и угла phi отклонения стержня от вертикали.

Далее определяем потенциальную энергию системы, которая имеет две составляющие: энергию сжатия пружины V1() и энергию шарика в поле тяжести V2(). Энергия деформации пружины определяется смещением пружины х относительно положения равновесия.
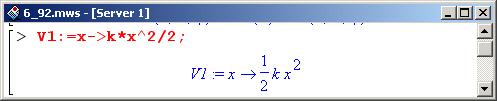
При отклонении стержня на угол phi приращение потенциальной энергии шарика, как известно, определяется следующим образом.

Суммарная потенциальная энергия зависит как от смещения бруска х относительно положения равновесия, так и от угла отклонения стержня phi относительно вертикали.

Теперь можно определить и функцию Лагранжа, которая, как уже упоминалось, равна разности кинетической и потенциальной энергий системы.

Для дальнейшего анализа удобно присвоить выражение для функции Лагранжа системы в качестве значения переменной Lg. При этом обобщенными координатами являются смещение х бруска относительно положения равновесия и угол отклонения стержня phi от вертикали. Соответственно, скорость бруска v является производной по времени от х, а угловая скорость omega – производной по времени от phi.

Чтобы по функции Лагранжа определить уравнения движения системы, необходимо вычислить частные производные от функции Лагранжа по каждой из ее переменных – всего четыре выражения. Каждое такое выражение присвоим в качестве значения элементам таблицы А, индексы которых будут обозначать переменную, по которой вычислялась производная.
