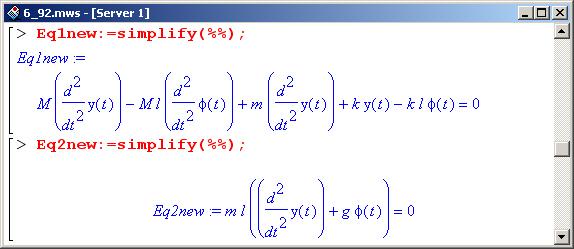Нахождение функции Лагранжа системы и частоты малых колебаний
Полученную таким образом систему из двух дифференциальных уравнений решить крайне проблематично, поэтому прибегнем к последующим решениям.

Упрощенную таким образом систему уравнений можно решить в общем виде. Ниже на этот случай приведена соответствующая команда. Результат ее выполнения, из которого можно определить частоты колебаний, не приводится в силу его исключительной громоздкости.

Однако для определения частот систему дифференциальных уравнений можно и не решать.
Для начала сделаем в уравнениях замену: вместо функции x(t) будем пользовать y(t), которая связана со "старыми" координатами х и phi соотношением y(t)=x(t)+1*phi(t). Фактически y(t) – это координата (горизонтальная) шарика в неподвижной системе координат.
Таким образом, получаем следующее.

Это уравнение неплохо было бы упростить.