Аналитическое дифференцирование. Аналитическое дифференцирование функции.
Операция дифференцирования реализована в Mathcad как в численной, так и в аналитической форме и обозначается при помощи традиционного оператора, т. е. соответствующими математическими символами (подобно сложению или умножению). Если расчеты выполняются с помощью вычислительного процессора, необходимо хорошо представлять себе особенности численного алгоритма, действие которого остается для пользователя "за кадром". С помощью Mathcad можно вычислять производные скалярных функций любого количества аргументов, причем как функции, так и аргументы могут быть и действительными, и комплексными.
Вне всякого сомнения, вы по достоинству оцените возможности символьного процессора, позволяющего с легкостью выполнять рутинные вычисления производных громоздких функций. В отличие от всех других операций, символьное дифференцирование выполняется успешно для подавляющего большинства аналитически заданных функций. Думаю, что многие читатели, которым иногда приходится аналитически дифференцировать функции, как и автор этих строк, единожды попробовав сделать это в среде Mathcad, уже никогда не возьмут в руки карандаша для расчета производных "вручную".
Аналитическое дифференцирование функции
Для того чтобы аналитически найти производную функции f (х) в Mathcad:
- Задайте функцию f (х).
- Введите оператор дифференцирования нажатием кнопки Derivative (Производная) на панели Calculus (Вычисления) или введите с клавиатуры вопросительный знак ?.
- В появившихся местозаполнителях оператора дифференцирования (рис. 3.1) введите функцию, зависящую от аргумента х, т. е. f(х), и имя самого аргумента х.
- Введите оператор › символьного вычисления для получения ответа (листинг 3.1).
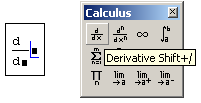
Рис. 3.1. Оператор дифференцирования
Листинг 3.1. Пример аналитического дифференцирования:
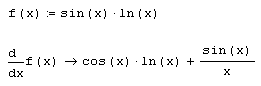
Примечание 1
Помните о том, что в описанном применении оператора дифференцирования его результатом является функция той же переменной х. Пример визуализации операции дифференцирования с помощью графика приведен на рис. 3.2.
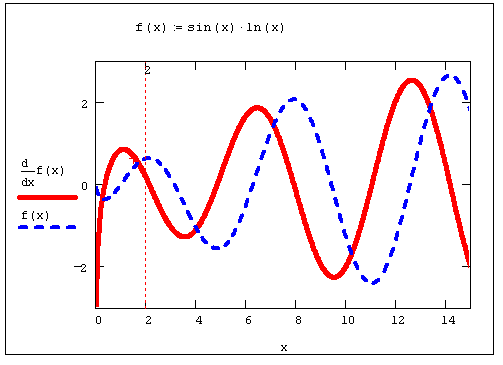
Рис. 3.2. График производной функции
Примечание 2
Исходная функция может зависеть не только от аргумента х, но и от других аргументов, например f(x,y,z,t) и т. п. В этом случае дифференцирование производится точно так же, причем становится более понятной необходимость определения переменной дифференцирования (в нижнем местозаполнителе оператора дифференцирования). Расчеты производных по разным аргументам (в этом случае говорят о частных производных), разумеется, будут давать совершенно разные результаты (см. разд. 3.4.).
