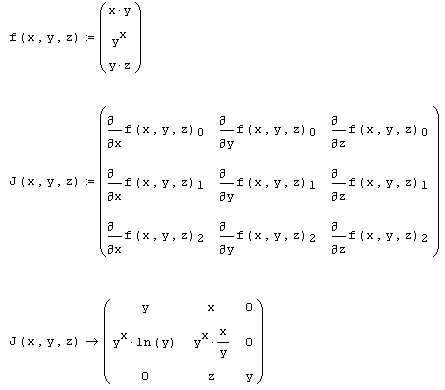Пример: якобиан
Еще одна задача, связанная с нахождением частных производных векторной функции, заключается в вычислении якобиана (или определителя матрицы Якоби) – матрицы, составленной из частных производных векторной функции по всем ее аргументам. Эта задача встречается в различных областях математики, например, применительно к жестким дифференциальным уравнениям (см. разд. 9.4). Приемы вычисления якобиана векторной функции f (х) векторного аргумента х демонстрируются в листинге 3.19. В нем для определения частных производных якобиана каждый i-й скалярный компонент f (x)i дифференцируется символьным процессором Mathcad.
Листинг 3.19. Вычисление якобиана векторной функции векторного аргумента:
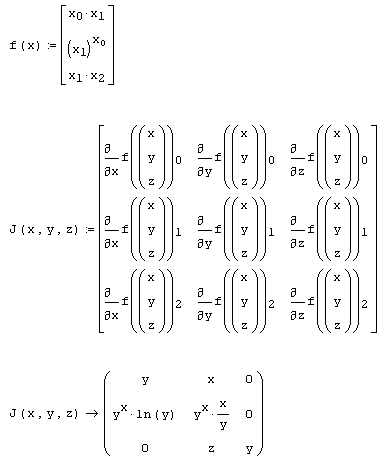
Тот же самый якобиан можно вычислить и несколько по-другому, если определить функцию не одного векторного, а трех скалярных аргументов f(x,y,z) (листинг 3.20). Не забывайте, что для численного определения якобиана необходимо сначала определить точку, в которой он будет рассчитываться, т. е. вектор х в терминах листинга 3.19, или все три переменных х, у, z в обозначениях листинга 3.20.
Листинг 3.20. Вычисление якобиана векторной функции трех скалярных аргументов: