Примеры: градиент, дивергенция и ротор
Как можно убедиться, сравнив графики на рис. 3.9 и 3.10, математический смысл градиента состоит в задании в каждой точке (х,у) направления на плоскости, в котором функция f (х,у) растет наиболее быстро. Абсолютное значение градиента (т. е. длина вектора в каждой точке) определяет локальную скорость изменения f (x,y). Из сопоставления графи ков ясно, что в центре показанной на них области (х,у) сама функция f (х,у) меняется медленно (соответственно, значения ее градиента являются малыми), а в углах – быстро (там значения градиента максимальны).
Очень важно заметить, что градиент является не скалярной, а векторной функцией переменных х,у, поскольку фактически представляет собой комбинацию двух функций, задающих соответствующие проекции (горизонтальную и вертикальную) вектора в каждой точке. До сих пор в данной главе мы рассматривали дифференцирование скалярных функций, однако в математике часто приходится иметь дело и с вычислением производных векторных функций. Рассмотрим эти действия на примере операции поиска дивергенции (листинг 3.15 и рис. 3.11), применимой к векторному полю, т. е. векторной функции, зависящей от пространственных координат (на плоскости, как в нашем примере, или в трехмерном пространстве).
Листинг 3.15. Вычисление дивергенции векторной функции:
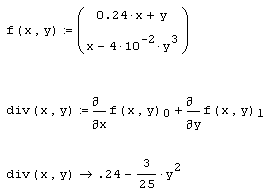
Если, как принято в математике, обозначить оператор взятия градиента символом V, то дивергенцию вектор-функции можно формально определить как скалярное произведение Vf, а еще одну распространенную операцию векторного анализа – ротор (или, по-другому, вихрь или завихренность) – как векторное произведение Vxf. Рис. 3.11 иллюстрирует пример векторной функции f (х,у) (определяемой в первой строке листинга) и вычисление ее дивергенции (которое производится аналитически в третьей строке). Обратите внимание, что в качестве исходной вектор-функции взят результат предыдущих расчетов, показанный (в форме векторного поля) на рис. 3.10. Строки кода в верхней части рис. 3.11 нужны для подготовки графика вычисленной дивергенции (в виде трехмерной поверхности и линий уровня, соответственно сверху и снизу).
Точно такую же структуру имеют расчеты ротора той же векторной функции f (х,у) в листинге 3.16, причем определение операции взятия ротора приводится в его второй строке (как и в случае дивергенции для листинга 3.15).
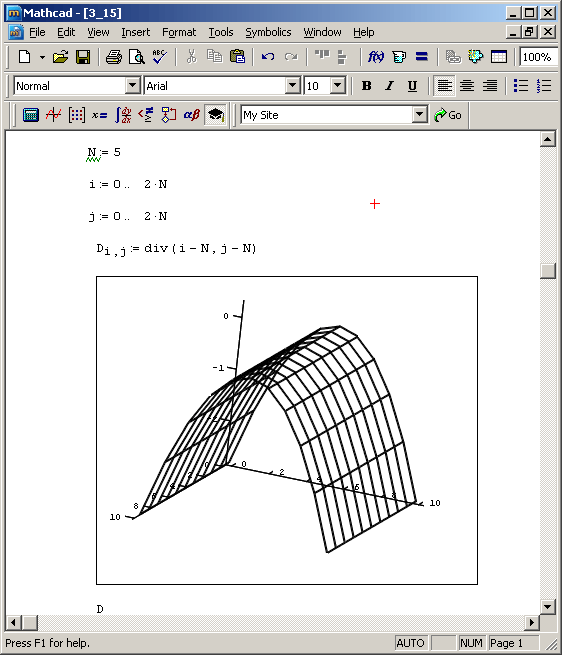
Рис. 3.11. График дивергенции векторной функции (продолжение листинга 3.15)
