Об алгоритме дифференцирования
Для численного дифференцирования Mathcad применяет довольно сложный алгоритм, вычисляющий производную с колоссальной точностью до 7-8-го знака после запятой. Погрешность дифференцирования не зависит от констант TOL или CTOL, в противоположность большинству остальных численных методов, а определяется непосредственно алгоритмом. Этот алгоритм (метод Риддера) описан во встроенной справочной системе Mathcad, доступной через меню Help (Справка). Мы не будем здесь его описывать, однако остановимся на важных аспектах численного определения производной функции f (х) на более простом примере. Несмотря на то, что простейшая разностная формула сильно отличается от метода Риддера, он все-таки поможет нам разобраться в некоторых вопросах, т. к. основан на базовом принципе численного дифференцирования, а именно на вычислении производной через значения функции f (х) в нескольких точках, расположенных на близком расстоянии друг от друга.
Исходя из определения производной функции, можно констатировать, что:
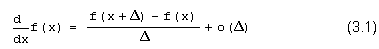
Основная проблема численного определения производной (как в этой простейшей формуле, так и в более сложных алгоритмах, в том числе Риддера) связана как раз с процедурой выбора значения Д, которая является далеко не очевидной. На первый взгляд может показаться, что следует выбирать очень малые Д, чтобы соблюсти желаемую точность, однако это не совсем так. Чтобы лучше разобраться в сути проблемы, используем Mathcad-программу, приведенную в листинге 3.6, которая рассчитывает (в зависимости от шага Д) погрешность разностной формулы (3.1). График полученной зависимости изображен на рис. 3.5, причем для его обеих осей выбран логарифмический масштаб, а сама производная (ради примера), согласно листингу 3.6, считается в одной точке х=1.
Листинг 3.6. Расчет зависимости точности разностной формулы от шага:
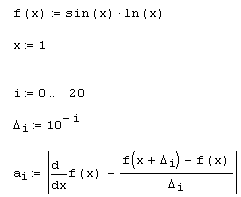
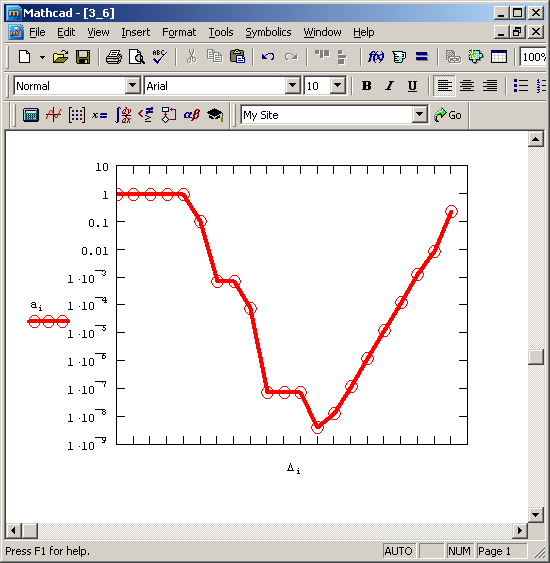
Рис. 3.5. График точности формулы (3.1) в зависимости от шага дельта (продолжение листинга 3.6)
