Производные высших порядков
Mathcad позволяет численно определять производные высших порядков, от 3-го до 5-го включительно. Чтобы вычислить производную функции f (х) N-го порядка в точке х, нужно проделать те же самые действия, что и при взятии первой производной (см. разд. 3.1 и 3.2), за тем исключением, что вместо оператора производной необходимо применить оператор n-й производной (Nth Derivative). Этот оператор вводится с той же панели Calculus (Вычисления), либо с клавиатуры нажатием клавиш CTRL +?, и содержит еще два дополнительных местозаполнителя (рис. 3.7), в которые следует поместить число N. В полном соответствии с математическим смыслом оператора, определение порядка производной в одном из местозаполнителей приводит к автоматическому появлению того же числа в другом из них.
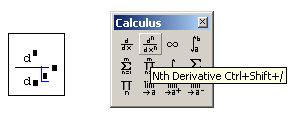
Рис. 3.7. Оператор производной высшего порядка
Очевидно, что "производная" при N=0 по определению равна самой функции, при N=1 получается обычная первая производная. Листинг 3.7 демонстрирует численное и символьное вычисление второй производной функции в заданной точке. Обратите внимание, что, как и при вычислении обычной производной, необходимо перед оператором дифференцирования присвоить аргументу функции значение, для которого будет вычисляться производная. А вот для аналитического нахождения производных высших порядков при помощи оператора символьного вывода (в полном соответствии с разд. 3.1), вводить значения аргумента не следует (листинг 3.8).
Листинг 3.7. Пример вычисления второй производной функции в точке:
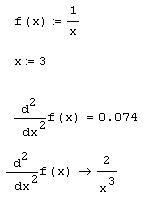
Листинг 3.8. Пример аналитического поиска второй производной функции:
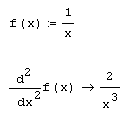
Примечание
Убедиться в том, что символьный процессор Mathcad в последней строке листинга 3.7 дает тот же результат, что и вычислительный процессор в предыдущей строке, можно, упростив его. Для этого следует выделить полученное последнее выражение и выбрать в меню Symbolics (Символика) пункт Simplify (Упростить). После этого ниже появится еще одна строка с численным результатом выделенного выражения.
Повторимся, что численный метод предусматривает возможность вычисления производных до 5-го порядка, а символьный процессор умеет считать производные произвольного порядка (конечно, если аналитическое решение задачи в принципе существует). Сказанное иллюстрирует листинг 3.9, в котором аналитически вычисляется шестая производная функции, а попытка численного вывода результата того же выражения приводит к ошибке.
Листинг 3.9. Численное и символьное вычисление шестой производной:
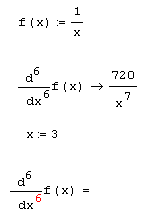
Чтобы вычислить производную порядка выше 5-го численно, можно последовательно применить несколько раз оператор м-й производной (листинг 3.10), подобно тому, как производится отыскание кратных интегралов (см. разд. 4.3.4). Однако следует помнить о том, что численное определение производных высших порядков производится тем же вычислительным методом Риддера, что и для первых производных. Поскольку, как уже было сказано, для первой производной этот метод обеспечивает точность до 7-8 значащих разрядов числа, при повышении порядка производной на каждую единицу точность падает примерно на один разряд.
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Зарегистрироваться и Начать продвижение
Внимание!
Из сказанного ясно, что падение точности при численном расчете высших производных может быть очень существенно. В частности, если попытаться определить шестую производную функции l/х, то в качестве результата будет выдан ноль, в то время как истинное значение девятой производной может быть найдено при помощи символьного процессора (листинг 3.10).
Листинг 3.10. Попытка численного поиска шестой производной функции в точке дает неправильный результат: