Разложение функции в ряд Тейлора. Разложение в ряд при помощи меню.
Еще одна операция, тесно связанная с дифференцированием, представляет собой разложение функции в ряд Тейлора по любой переменной х в некоторой точке. Если эта точка х=0, то ряд называют также рядом Маклорена, и он представим в окрестности точки х=0 суммой вида a0+a1x+a2x2+a3x3+… Здесь ai – некоторые коэффициенты, не зависящие от х, но, возможно, являющиеся функциями других переменных, от которых зависит исходная функция. Именно эти коэффициенты выражаются через производные функции. Если она имеет в точке х=0 особенность, то соответствующее разложение называют рядом Лорана.
При поиске разложения в ряд Тейлора нет необходимости явно рассчитывать все его коэффициенты, поскольку эта операция предусмотрена разработчиками Mathcad и выполняется при помощи символьного процессора. При этом можно использовать для ее осуществления как соответствующие встроенные функции, так и меню Symbolics (Символика).
Разложение в ряд при помощи меню
Чтобы разложить некоторое выражение в ряд:
- Введите выражение.
- Выделите значение переменной, по которой требуется получить разложение в ряд.
- Выполните команду Symbolics › Variable › Expand to Series (Символика › Переменная › Разложить в ряд) (рис. 3.12).
- В появившемся диалоговом окне Expand to Series (Разложить в ряд) введите желаемый порядок аппроксимации (Order of Approximation) и нажмите кнопку ОК.
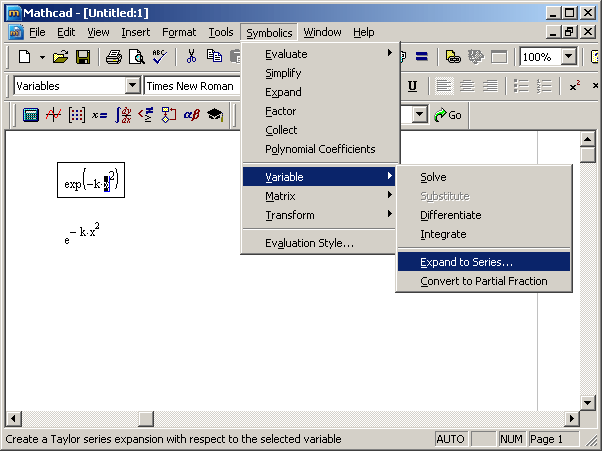
Рис. 3.12. Аналитическое разложение выражения в ряд по переменной х
Результат разложения появится под выражением (он показан на рис. 3.12, внизу).
Примечание
Не забывайте, что разложение строится только в точке х=0. Чтобы получить разложение в другой точке х=а, можно, к примеру, подставить вместо переменной х значение х-а.
