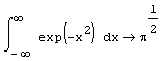Определенный интеграл. Оператор интегрирования.
С одной стороны, численное интегрирование – одна из самых простых, с вычислительной точки зрения, операций, с другой – аналитически проинтегрировать можно далеко не каждую функцию. Всегда помните об этом, когда вы сталкиваетесь с численным или аналитическим интегрированием.
Интегрирование в Mathcad реализовано в виде вычислительного оператора. Допускается вычислять интегралы от скалярных функций в пределах интегрирования, которые также должны быть скалярными. Несмотря на то, что пределы интегрирования обязаны быть действительными, подынтегральная функция может иметь и комплексные значения, поэтому и значение интеграла может быть комплексным.
Оператор интегрирования
Интегрирование, как и дифференцирование, и множество других математических действий, устроено в Mathcad по принципу "как пишется, так и вводится". Чтобы вычислить определенный интеграл, следует напечатать его обычную математическую форму в документе. Делается это с помощью панели Calculus (Вычисления) нажатием кнопки со значком интеграла или вводом с клавиатуры сочетания клавиш SHIFT + 7 (или символа "&", что то же самое). Появится символ интеграла с несколькими местозаполнителями (рис. 4.1), в которые нужно ввести нижний и верхний интервалы интегрирования, подынтегральную функцию и переменную интегрирования.
Примечание
Если пределы интегрирования имеют размерность, то она должна быть одной и той же для обоих пределов.
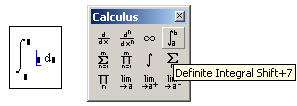
Рис. 4.1. Оператор интегрирования
Чтобы получить результат интегрирования, следует ввести знак равенства или символьного равенства. В первом случае интегрирование будет проведено численным методом, во втором – в случае успеха будет найдено точное значение интеграла с помощью символьного процессора Mathcad. Эти два способа иллюстрирует листинг 4.1. Конечно, символьное интегрирование возможно только для сравнительно небольшого круга несложных подынтегральных функций.
Листинг 4.1. Численное и символьное вычисление определенного интеграла:
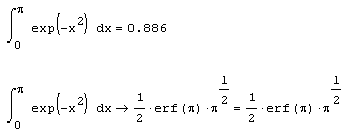
Примечание 1
Можно вычислять интегралы с одним или обоими бесконечными пределами (листинг 4.2). Для этого на месте соответствующего предела введите символ бесконечности, воспользовавшись, например, той же самой панелью Calculus (Вычисления). Чтобы ввести (минус бесконечность), добавьте знак минус к символу бесконечности, как к обычному числу.
Листинг 4.2. Вычисление интеграла с бесконечными пределами: