Иллюстрированный самоучитель по MathCAD 12

Дискретное преобразование Фурье

В предыдущем разделе рассказывалось о возможностях символьного процессора Mathcad, позволяющего осуществить аналитическое преобразование Фурье функции, заданной формулой. Между тем огромный пласт задач вычислительной математики связан с расчетом интегралов Фурье для функций, либо заданных таблично (например, представляющих собой результаты какого-либо эксперимента), либо функций, проинтегрировать которые аналитически не удается. В данном случае вместо символьных преобразований приходится применять численные методы интегрирования, связанные с дискретизацией подынтегральной функции и называемые потому дискретным Фурье-преобразованием.

В численном процессоре Mathcad дискретное преобразование Фурье реализовано при помощи популярнейшего алгоритма быстрого преобразования Фурье (сокращенно БПФ). Этот алгоритм реализован в нескольких встроенных функциях Mathcad, различающихся только нормировками:

• fft(y) – вектор прямого преобразования Фурье;
• FFT (у) – вектор прямого преобразования Фурье в другой нормировке;
• ifft (w) – вектор обратного преобразования Фурье;
• IFFT (w) – вектор обратного преобразования Фурье в другой нормировке:
  • у – вектор действительных данных, взятых через равные промежутки значений аргумента;
  • w – вектор действительных данных Фурье-спектра, взятых через равные промежутки значений частоты.

Внимание!
Аргумент прямого Фурье-преобразования, т. е. вектор у, должен иметь ровно 2ⁿ элементов (n – целое число). Результатом является вектор с 1+2^n-1 элементами. И наоборот, аргумент обратного Фурье-преобразования должен иметь 1+2^n-1 элементов, а его результатом будет вектор из 2ⁿ элементов. Если число данных не совпадает со степенью 2, то необходимо дополнить недостающие элементы нулями.

В листинге 4.14 показан пример расчета Фурье-спектра для модельной функции f (x), представляющей собой сумму двух синусоид разной амплитуды (верхний график на рис. 4.10). Расчет проводится по N=128 точкам, причем предполагается, что интервал дискретизации данных у_i равен h. В предпоследней строке листинга корректно определяются соответствующие значения частот W, а в последней применяется встроенная функция FFT. Полученный график Фурье-спектра показан на рис. 4.10 (снизу). Обратите внимание, что результаты расчета представляются в виде его модуля, поскольку сам спектр, как уже отмечалось, является комплексным. Очень полезно сравнить полученные амплитуды и местоположение пиков спектра с определением синусоид в начале листинга.

Примечание
Более подробную информацию о свойствах и практике применения Фурье-преобразования вы найдете в главе 14.

Листинг 4.14. Дискретное преобразование Фурье (алгоритм БПФ) модельного сигнала:

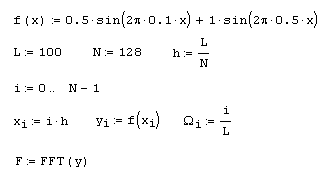
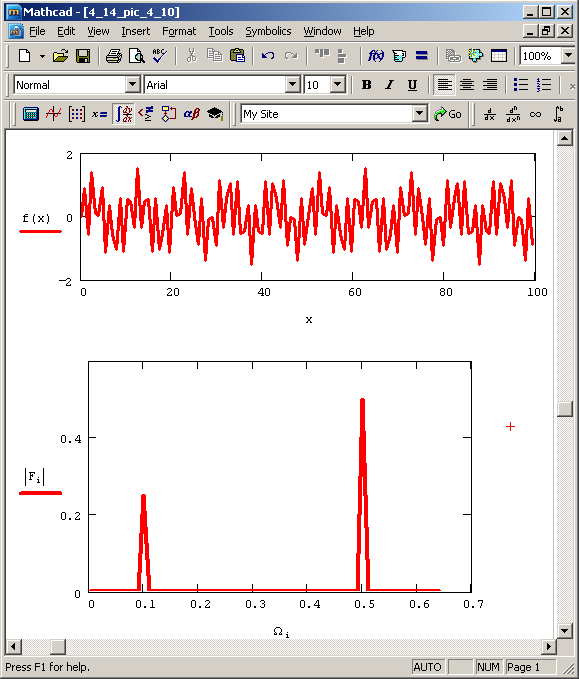
Рис. 4.10. Модельная функция и ее преобразование Фурье (продолжение листинга 4.14)