Преобразование Фурье комплексных данных
Алгоритм быстрого преобразования Фурье для комплексных данных встроен в соответствующие функции, в название которых входит литера "с":
- cfft(y) – вектор прямого комплексного преобразования Фурье;
- CFFT(y) – вектор прямого комплексного преобразования Фурье в другой нормировке;
- icfft(y) – вектор обратного комплексного преобразования Фурье;
- ICFFT(w) – вектор обратного комплексного преобразования Фурье в другой нормировке:
- у – вектор данных, взятых через равные промежутки значений аргумента;
- w – вектор данных Фурье-спектра, взятых через равные промежутки значений частоты.
Функции действительного преобразования Фурье используют тот факт, что в случае действительных данных спектр получается симметричным относительно нуля, и выводят только его половину (см. разд. 4.4.3). Поэтому, в частности, по 128 действительным данным получалось всего 65 точек спектра Фурье. Если к тем же данным применить функцию комплексного преобразования Фурье (рис. 4.11), то получится вектор из 128 элементов.
Сравнивая рис. 4.10 и 4.11, можно уяснить соответствие между результатами действительного и комплексного Фурье-преобразования.
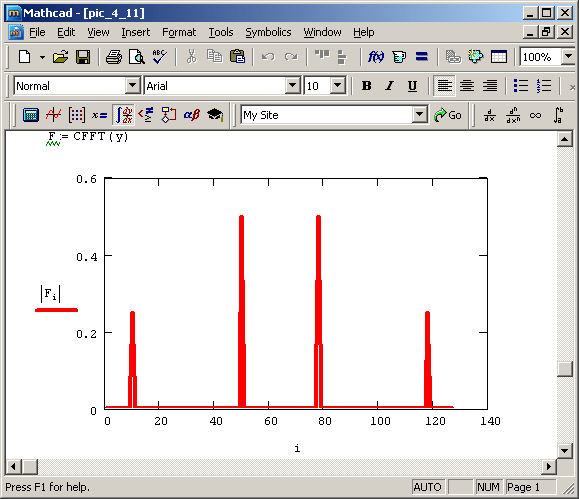
Рис. 4.11. Комплексное преобразование Фурье (продолжение листинга 4.14)
