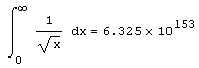Интегралы специального вида
Завершим разговор о приемах интегрирования в среде Mathcad примерами вычислений в некоторых специальных случаях, которые довольно часто встречаются в самых разнообразных областях математики.
Интегралы с бесконечными пределами
Как мы уже говорили (см. примечание 1 в разд. 4.1.1 и листинг 4.2), для того, чтобы вычислить определенный интеграл с одним или обоими бесконечными пределами, достаточно ввести, пользуясь панелью Calculus (Вычисления), специально предусмотренный разработчиками символ бесконечности в нужные местозаполнители интервалов интегрирования.
Расходящиеся интегралы
Если интеграл расходится (равен бесконечности), то вычислительный процессор Mathcad может выдать сообщение об ошибке, выделив при этом оператор интегрирования, как обычно, красным цветом. Чаще всего ошибка будет иметь тип "Found a number with a magnitude greater than 10307 " (Найдено число, превышающее значение 10307) или "Can't converge to a solution" (Не сходится к решению). Листинг 4.6 демонстрирует невозможность численного расчета интеграла(нижняя строка листинга). Тем не менее символьный процессор справляется с этим интегралом, совершенно правильно находя его бесконечное значение (верхняя строка листинга 4.6).
Листинг 4.6. Вычисление расходящегося интеграла:
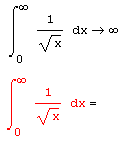
При попытке численного решения задачи листинга 4.6 методом, отличным от алгоритма вычисления интегралов с бесконечными пределами (Infinite Limit), получится неверное решение (листинг 4.7). А именно, вместо бесконечности будет выдано большое, но конечное число, немного не дотягивающее до численной бесконечности, являющейся для вычислительного процессора просто большим числом 10307. Отметим, что Mathead в режиме автоматического выбора алгоритма (AutoSelect) предлагает для интегралов с бесконечным пределом именно алгоритм Infinite Limit.
Листинг 4.7. Плохо выбранный численный алгоритм (в данном случае, адаптивный) неверно находит расходящийся интеграл: