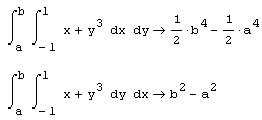Интегралы специального вида
Интеграл с переменным пределом
Символьный процессор предоставляет замечательные возможности аналитического вычисления интегралов, в том числе зависящих от параметров. Особую важность имеет вычисление интеграла с переменным пределом (верхним или нижним), для которого один из пределов интегрирования является переменной, отличной от переменной интегрирования (листинг 4.8). Нетрудно сообразить, что, с точки зрения символьного процессора, интеграл с переменным пределом является обычным определенным интегралом, зависящим от дополнительного параметра.
Листинг 4.8. Аналитическое вычисление интеграла с переменным верхним пределом:
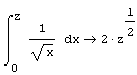
Кратные интегралы
Кратным называется интеграл функции многих переменных, берущийся по нескольким переменным. Для того чтобы вычислить кратный интеграл:
- Введите, как обычно, оператор интегрирования.
- В соответствующих местозаполнителях введите имя первой переменной интегрирования и пределы интегрирования по этой переменной.
- На месте ввода подынтегральной функции введите еще один оператор интегрирования (рис. 4.7).
- Точно так же введите вторую переменную, пределы интегрирования и подынтегральную функцию (если интеграл двукратный) или следующий оператор интегрирования (если более чем двукратный) и т. д., пока выражение с многократным интегралом не будет введено окончательно.
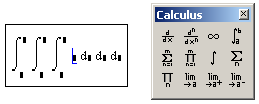
Рис. 4.7. Ввод нескольких операторов интегрирования для расчета кратного интеграла
Пример символьного и численного расчета двукратного интеграла в бесконечных пределах приведен в листинге 4.9. Обратите внимание, что символьный процессор "угадывает" точное значение интеграла л, а вычислительный определяет его приближенно и выдает в виде числа 3.142.
Листинг 4.9. Символьное и численное вычисления кратного интеграла:
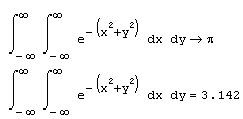
Внимание!
Аккуратнее вводите в редакторе Mathcad кратные интегралы, если они имеют различные пределы интегрирования по разным переменным. Не перепутайте пределы, относящиеся к разным переменным. Если вы имеете дело с такого рода задачами, обязательно разберитесь с листингом 4.10, в котором символьный процессор вычисляет двукратный интеграл. В первой строке пределы интегрирования [а,b] относятся к переменной у, а во второй строке – к переменной X.
Листинг 4.10. Символьное вычисление кратных интегралов: