Неопределенный интеграл
Предыдущий раздел был посвящен проблеме поиска определенного интеграла, т. е. числового значения, равного площади фигуры, образованной графиком подынтегральной функции и.осью х (см. рис. 4.4). Задача нахождения неопределенного интеграла намного сложнее, поскольку связана с поиском функции, производная от которой равна исходной подынтегральной функции. Решение этой задачи целиком возложено на символьный процессор Mathcad.
Символьное интегрирование
Для того чтобы аналитически проинтегрировать некоторую функцию, следует ввести с панели Calculus (Вычисления) символ неопределенного интеграла, в появившемся в документе шаблоне заполнить местозаполнители и, наконец, ввести знак символьного равенства. В случае успеха по истечении некоторого времени расчетов справа от введенного выражения появится его аналитический результат (листинг 4.4). Если же функцию не удается проинтегрировать аналитически, введенное вами выражение будет просто продублировано (листинг 4.5).
Примечание
Помните, что при символьном интегрировании допускается использовать в выражениях, которые вы вводите, различные параметры. Если перед выражением вы нигде не определяли их значения, то (в случае успешных вычислений) символьный процессор Mathcad выдаст аналитическую зависимость результата интегрирования от этих параметров (как в листинге 4.4 от параметра а).
Листинг 4.4. Аналитическое вычисление неопределенного интеграла:
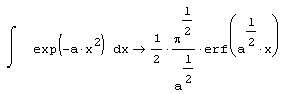
Листинг 4.5. Аналитическое интегрирование невозможно:
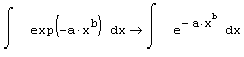
Интегрирование при помощи меню
Для вычисления неопределенного интеграла от некоторого выражения по определенной переменной при помощи меню выделите в выражении переменную и выполните команду Symbolics › Variable › Integrate (Символика › Переменная › Интегрировать) (рис. 4.6). Вычисленное аналитическое представление неопределенного интеграла появится ниже. При этом результат может содержать как встроенные в Mathcad функции, так и другие спецфункции, которые нельзя непосредственно рассчитать в Mathcad, но символьный процессор "умеет" выдавать их в качестве результата некоторых аналитических операций.
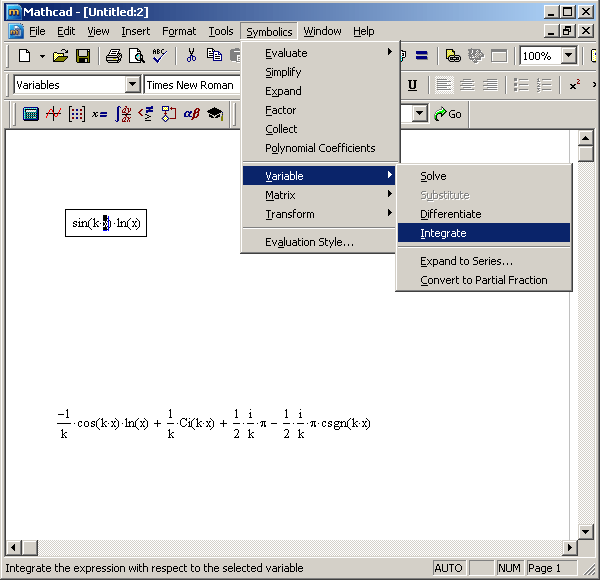
Рис. 4.6. Интегрирование выражения по переменной при помощи меню
