Другие интегральные преобразования. Преобразование Лапласа.
Рассмотрим в завершение главы, посвященной интегрированию, еще три преобразования, которые часто применяются помимо интеграла Фурье. Отметим, что преобразование Лапласа и Z-преобразование встречаются в практических задачах вычислительной математики относительно редко, а вот вейвлет-преобразование, теория которого появилась относительно недавно, постепенно выходит на лидирующие позиции в проблемах обработки данных.
Преобразованием Лапласа называют интеграл от f (х) следующего вида:
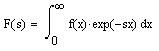
Рассчитывается преобразование Лапласа совершенно аналогично Фурье-преобразованию (см. разд. 4.4). Примеры преобразования Лапласа приведены в листинге 4.16 и на рис. 4.13.
Листинг 4.16. Двумерное преобразование Лапласа:

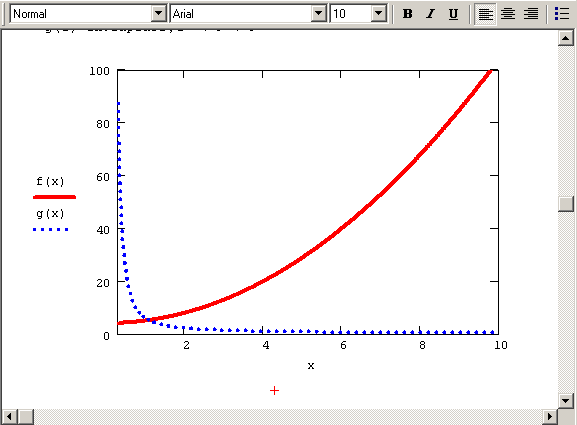
Рис. 4.13. Прямое и обратное преобразование Лапласа (продолжение листинга 4.16)
