Интеграл Фурье. Об интегральных преобразованиях функций.
Обратимся теперь к характерным проблемам вычислительной математики, связанным с (аналитическим или численным) вычислением интегралов определенного вида. Задачи, о которых мы собираемся рассказать, тесно связаны с алгоритмами обработки данных, поэтому содержание этого раздела будет перекликаться с материалом главы 14 (см. разд. 14.1). Благодаря обширному применению для вычисления таких интегралов разработаны специфические алгоритмы, несравненно более эффективные, чем традиционные (см. разд. 4.1.4), причем некоторые из них имеются в арсенале Mathcad в форме встроенных функций вычислительного процессора и соответствующих операций символьного процессора.
Наиболее широко распространенным интегральным преобразованием является преобразование Фурье, которое представляет функцию f (х) в виде интеграла по гармоническим функциям, называемого интегралом Фурье:
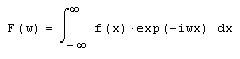
Функция F(co) называется также преобразованием Фурье, или Фурье-спектром исходной функции f (х). Ее аргумент ш имеет смысл частоты соответствующей гармонической составляющей f (х). Важно отметить, что функция, выражающая преобразование Фурье, комплексна, даже если f(x) является действительной.
Об интегральных преобразованиях функций
Вообще говоря, интегральные преобразования по определению ставят в соответствие некоторой функции f (х) другую функцию от другого аргумента F(w). Причем это соответствие f (x) › F(co) задается интегральной зависимостью. Символьный процессор Mathcad позволяет осуществлять три вида интегральных преобразований функций – преобразование Фурье, Лапласа и Z-преобразование. Наряду с прямыми преобразованиями имеется возможность совершать любое из этих трех обратных преобразований, т. е. F(w) › f (x).
Аналитически все интегральные преобразования выполняются аналогично символьному интегрированию (см. разд. 4.2.2). Для вычисления преобразования выражения выделяется переменная, по которой будет осуществляться преобразование, и затем выбирается соответствующий пункт меню. Преобразования с применением оператора символьного вывода используются с одним из соответствующих ключевых слов, вслед за которым требуется указать имя нужной переменной.
Приведем примеры символьного расчета каждого из трех интегральных преобразований, а также расскажем о численных методах Фурье и вейвлет-преобразований.
