Иллюстрированный самоучитель по MathCAD 12

О традиционных алгоритмах интегрирования

Прежде чем перейти к изложению метода численного интегрирования, реализованного в Mathcad, скажем несколько слов об основных принципах численного интегрирования. Исходя из геометрического смысла определенного интеграла функции f (х) как площади фигуры, образованной графиком этой функции и осью х, можно предложить самый простой способ интегрирования "хорошей" функции – применить формулу прямоугольников. С ее помощью площадь упомянутой искомой фигуры подсчитывается как сумма элементарных прямоугольников, множеством которых заменяется подынтегральная функция f (х).

Иллюстрация метода прямоугольников приведена на рис. 4.4. Для подсчета интеграла i интервал интегрирования [а,b] разбивается на N отрезков. На. каждом i-м отрезке f (х) заменяется прямоугольником с шириной h и высотой f (x_i). Площадь каждого из этих элементарных прямоугольников составляет hf (x_i), а их сумма s может считаться приближением к искомому интегралу I. Несложно показать, что при N › ~ множество элементарных прямоугольников стремится к искомой фигуре, образованной подынтегральной функцией, а значение S › I, причем погрешность (отличие s от точного значения i) составляет o(h²).

Можно воспринимать смысл алгоритма прямоугольников в замене исходной подынтегральной функции другой, близкой к ней (в данном случае, кусочно-непрерывной) функцией, интеграл от которой легко подсчитать аналитически. Принцип более точных методов интегрирования как раз и состоит в интерполяции подынтегральной функции f(х) некоторой близкой зависимостью у(х) и расчете интеграла уже от этой функции. Важно, чтобы при этом, во-первых, интеграл от у(х) мог быть точно рассчитан аналитическими методами; и, во-вторых, функция f(х) была бы по возможности ближе к у(х), чтобы уменьшить погрешность.

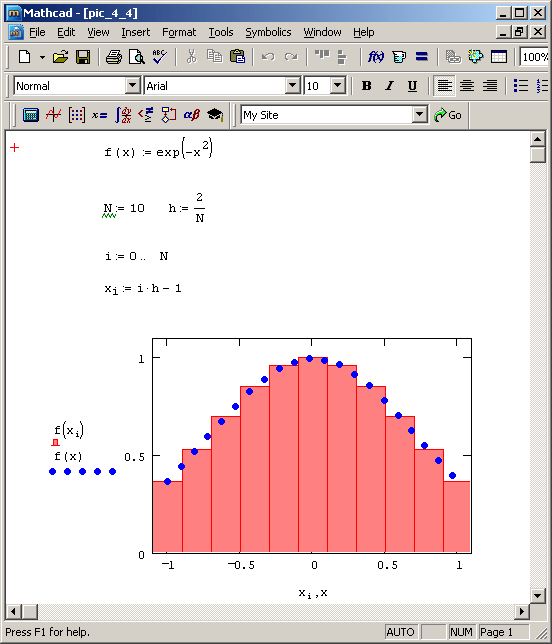
Рис. 4.4. Реализация алгоритма прямоугольников

Очевидно, что наиболее простой алгоритм заключается в интерполяции подынтегральной функции на каждом из N шагов интегрирования f (х) каким-либо полиномом у(х). Известно, что могут быть предложены различные пути построения интерполирующих полиномов, отличающихся, в частности, порядком. Например, полиномы Лагранжа строятся при интерполяции f (х) в n точках на каждом из N элементарных интервалов интегрирования. Семейство классических алгоритмов интегрирования в этом случае называется методами Ньютона-Котеса. Заметим, что при n=1 полиномом является прямая линия, и мы имеем метод трапеций; при n=2 интерполирующим полиномом на каждом шаге интегрирования будет квадратичная парабола, и мы получим алгоритм Симпсона и т. д.

Примечание
Дополнительные сведения об алгоритме полиномиальной интерполяции приведены в главе 13.