Интерполяция, аппроксимация и регрессия
Регрессия и визуализация ее результатов
Еще один широко используемый вид аппроксимации – регрессия. Она заключается в нахождении параметров некоторой функции регрессии, при которой график этой функции проходит в "облаке" узловых точек, обеспечивая наименьшую среднеквадратичную погрешность их представления. В отличие от интерполяции, при регрессии найденная функция не дает точного значения ординат в узловых точках – она просто минимизирует погрешность вычислений в этих точках.
Для решения задач регрессии используется функция ядра:
Fit: Fit[data, funs, vars]Эта функция ищет приближение для списка данных data методом наименьших квадратов в виде линейной комбинации функций funs переменных vars. Данные data могут иметь форму {{x1, y1,…, f1}, {х2, у2,…, f2 },…}, где число координат х, у,… равно числу переменных в списке vars. Также данные data могут быть представлены в форме {f 1, f 2, =..} с одной координатой, принимающей значения 1, 2… Аргумент funs может быть любым списком функций, которые зависят только от объектов vars.
Следующие примеры показывают приближение исходных данных степенным полиномом и линейной комбинацией двух функций:
Fit[{{0, 0.9}, {2, 8.099999999999999), {3, 17}, {4, 33}}, {a, x, x2}, x] 0. 997273-1.40864 x+2.33409 x2 Fit[{{0, 0.9}, {2, 8.099999999999999}, {3, 17}}, {x2, Exp[x], x}, x] 0.9ex + 2.89276x - 1.08392 x2Здесь в первом примере выполняется полиномиальная регрессия со степенью полинома, равной 2. Максимальная степень на 1 меньше числа пар исходной зависимости (в нашем случае их 4) – при такой степени регрессия вырождается в обычную полиномиальную аппроксимацию, которая рассматривалась ранее.
Рисунок 5.14 показывает несколько иной путь проведения полиномиальной аппроксимации – исходные данные заданы объектом-списком data.
В конце документа рис. 5.14 показано построение графика аппроксимирующего полинома второй степени и точек исходных данных. Заметно, что при регрессии график полинома проходит в середине "облака" исходных точек и не укладывается на них точно.
В уроке 12 будут рассмотрены дополнительные функции для проведения регрессии. Они входят в различные пакеты расширения системы Mathematica 3/4.
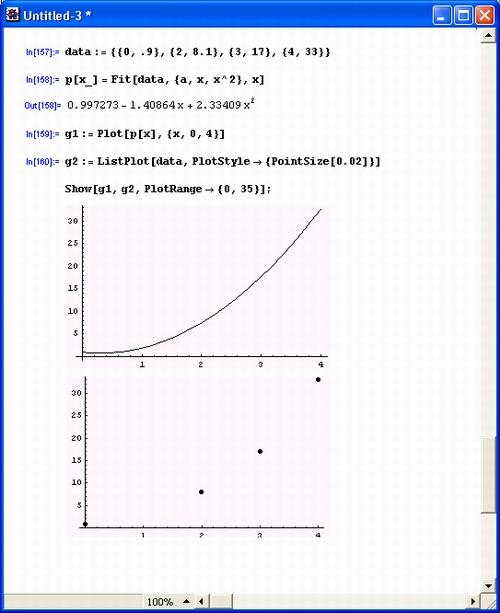
Рис. 5.14. Полиномиальная регрессия с графическим выводом
