Функции пакета FourierTransform
Подпакет FourierTransform пакета Calculus в версии Mathematics 3 служит для осуществления расширенных преобразований Фурье. Он вызывается командой:
<<Calculus'FourierTransform'Ввиду важности этих преобразований в системе Mathematica 4 их функции были размещены уже в ядре системы. Это следующие функции:
- FourierTransform [expr, t, w] – возвращает результат прямого преобразования Фурье над выражением expr [t], выраженного через переменную w;
- InverseFourierTransform[expr, w, t] – возвращает результат обратного преобразования Фурье над выражением expr[w], выраженного через переменную t;
- FourierCosTransform[expr, t, w] – возвращает результат косинусного преобразования Фурье над выражением expr [t ], выраженного через переменную w;
- FourierSinTransform[expr, t, w] – возвращает результат синусного преобразования Фурье над выражением expr [t], выраженного через переменную w;
- FourierTransform [expr, {tl,t2}, {wl, w2 } ] – возвращает результат прямого преобразования Фурье над выражением expr [ t1, t2,…], выраженного через переменные {w1, w2,-…};
- InverseFourierTransformtexpr, {tl,t2}, {wl,w2} ] – возвращает результат обратного преобразования Фурье над выражением expr [ wl, wl,…], выраженного через переменные {t1, t2,…}.,
Примеры осуществления прямого и обратного преобразований Фурье представлены ниже:
FourierTransform[Sin[t]*t:2, t, w] -In(DiracDelta``[1 - w] - DiracDelta``[1 + w]) InverseFourierTransform[%, w, t] t2Sin[t] FourierCosTransform[Sin[t]*t:2, t, w] -8w2/(1-w2)3-2/(1-w2)2 FourierSinTransform[Cos[a*t], t, w] -w/(a2-w2) FourierTransform[tl^2 Exp[-a t2] UnitStep[t1, t2], {t1, t2}, {w1, w2}] -2I/w13-nDiracDelta``[w1]/a-IW2 InverseFourierTransformtwl/(1-b*w2), {w1, w2}, {t1, t2}]Для реализации спектрального анализа и синтеза имеются следующие функции:
- FourierExpSeries [expr, {x, xmin, xmax), n] – возвращает разложение expr [х] в экспоненциальный ряд Фурье с n членами на отрезке {xmin, xmax};
- FourierExpSeriesCoef f icient [expr, {x, xmin, xmax},n] – возвращает коэффициенты разложения expr [x] в экспоненциальный ряд Фурье с n членами на отрезке {xmin, xmax};
- FourierTrigSeries [expr, {x, xmin, xmax}, n] – возвращает разложение expr [x] в тригонометрический ряд Фурье с n членами на отрезке {xmin, xmax};
- FourierSinSeriesCoef f icient [expr, {x, xmin, xmax}, n] – возвращает синусные коэффициенты разложения expr [x] в тригонометрический ряд Фурье с n членами на отрезке {xmin,xmax};
- FourierCosSeriesCoef f icient [expr, {x, xmin, xmax}, n] – возвращает косинусные коэффициенты разложения expr [x] в тригонометрический ряд Фурье с n членами на отрезке {xmin, xmax}.
Рисунок 5.12 иллюстрирует создание пилообразного сигнала, его разложение в тригонометрический ряд Фурье с n = 4, графическое воспроизведение сигнала и его представление суммой из четырех гармоник (на рисунке оставлены только совмещенные графики). Таким образом, последняя операция демонстрирует проведение синтеза пилообразного сигнала по четырем гармоникам.
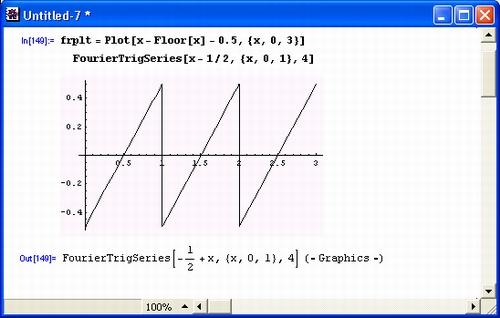
Рис. 5.12. Создание пилообразного сигнала, его разложение в тригонометрический ряд Фурье и синтез сигнала по четырем гармоникам
Помимо указанных функций существует целая группа функций для численных операций, связанных с разложением в ряд Фурье. Все они имеют в начале имени букву N, например:
- NFourierTrigSeries [expr, {x, xmin,xmax}, n] – возвращает разложение expr [ x ] в тригонометрический ряд Фурье с n членами на отрезке {xmin, xmax} в численном виде.
Предоставляем читателю опробовать эти функции самостоятельно.
