Учет искажений сигнала
Рисунок 5.20 показывает задание амплитудно-частотной и фазо-частотной (ФЧХ) характеристик некоего фильтра, ослабляющего высокие частоты и вносящего фазовый сдвиг, пропорциональный частоте сигнала. В нижней части рисунка построены эти характеристики. Заметим, что здесь АЧХ и ФЧХ заданы без "хитростей", присущих решению аналогичной задачи с применением встроенных функций дискретного преобразования Фурье. Они задаются в явном виде как функции от частоты.
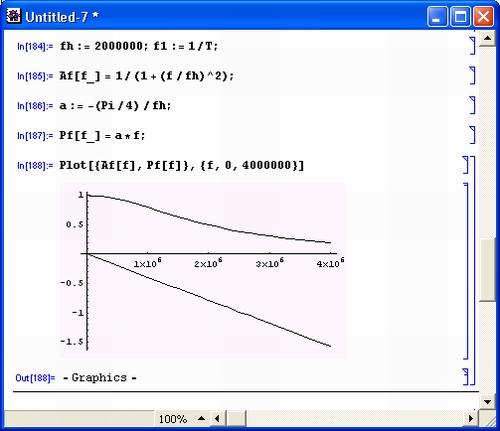
Рис. 5.20. Амплитудно-частотная и фазочастотная характеристики фильтра
Рисунок 5.21 показывает, как влияет на форму сигнала его прохождение через фильтрующую цепь. Для оценки этого используется формула синтеза гармоник. Однако отличные от нуля амплитуды гармоник умножаются на модуль коэффициента передачи (АЧХ) фильтра, а к фазе каждой гармоники добавляется фазовый сдвиг, вносимый фильтром (ФЧХ). Таким образом, в процессе синтеза временной зависимости сигнала учитываются амплитудно-частотные и фазо-частотные искажения сигнала фильтром.
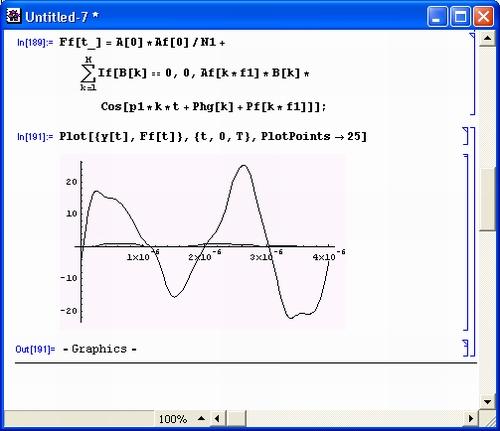
Рис. 5.21. Сравнение исходной временной зависимости сигнала и сигнала на выходе фильтрующей цепи
Рассмотренный документ является хорошей иллюстрацией применения системы Mathematica для решения нестандартных задач и реализации альтернативных методов их решения. В частности, в данном случае спектральный анализ и синтез велись по типичной для инженерных расчетов методике и без использования встроенных функций преобразования Фурье.
