Спектральный анализ с линейной интерполяцией сигнала
На рис. 5.17 крупным планом показано построение спектрограммы амплитуд гармоник заданного сигнала. Дабы подчеркнуть дискретность гармоник, амплитуда каждой из них показана точкой, около которой стоит номер гармоники. Для этого пришлось использовать графическую функцию LabeledListPlot из пакета расширения Graphics. Нетрудно заметить, что амплитуды гармоник быстро убывают по мере роста их номера. Однако, поскольку суммируется множество гармоник, это не является основанием для слишком поспешного отбрасывания высших гармоник.
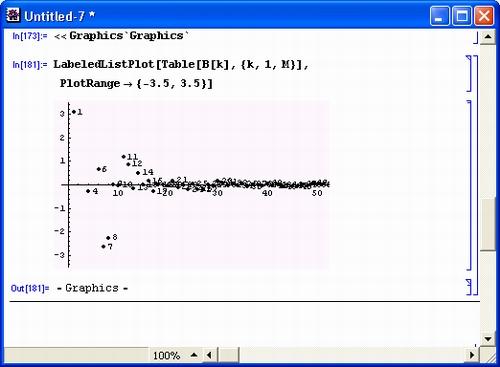
Рис. 5.17. Спектрограмма амплитуд гармоник
Рисунок 5.18 представляет спектрограмму фаз гармоник. Фазы гармоник также имеют дискретные значения и показаны точками с номерами. Значение фазового сдвига лежит в пределах от -n до n.
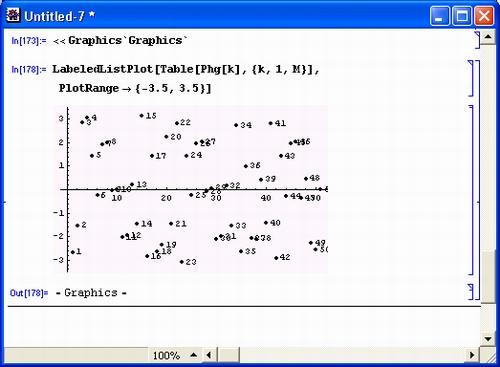
Рис. 5.18. Спектрограмма фаз гармоник
Теперь, получив набор гармоник заданного сигнала, можно приступить к его гapмоническому синтезу. Он представлен на рис. 5.19 сверху. Здесь также применен прием, иногда ускоряющий вычисления, – гармоники с нулевой амплитудой из формулы синтеза устраняются.
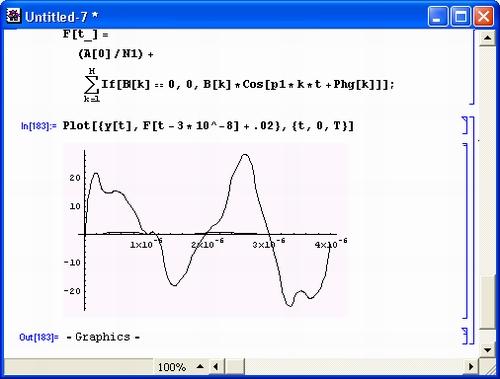
Рис. 5.19. Гармонический синтез сигнала и сравнение его результатов с временной зависимостью интерполированного сигнала
Самый "волнующий" момент представлен во второй части рис. 5.19 – здесь показано сравнение результата гармонического синтеза сигнала с его временной зависимостью (интерполированной). Чтобы исходный и синтезированный сигналы не сливались, синтезированный сигнал намеренно немного сдвинут вправо и вверх. Нетрудно заметить, что несмотря на сложный характер сигнала его гармонический (спектральный) синтез в данном случае дает превосходные результаты уже при использовании 51 гармоники (включая нулевую). Если убрать отмеченный выше сдвиг, то сигналы практически сливаются.
