Фильтрация сигналов на основе преобразований Фурье
Преобразование Фурье является теоретической основой фильтрации сложных сигналов. Мы рассмотрим комплексный пример на фильтрацию сигнала, представляющего собой функцию Бесселя первого рода третьего порядка. Рисунок 5.10 показывает верхнюю часть документа, демонстрирующую создание исходного сигнала и описание частотного фильтра.
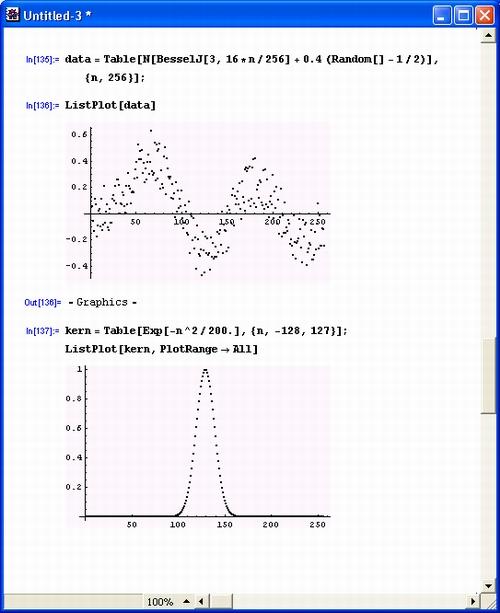
Рис. 5.10. Часть документа, показывающая создание сигнала и синтез фильтра для него
Как и в ранее рассмотренном примере, сигнал формируется как сумма чистого сигнала со случайной составляющей, моделирующей шум. Выбранная форма сигнала напоминает затухающую синусоиду. Уровень шумов выбран достаточно большим, так что форма чистого сигнала с трудом угадывается на фоне шумов (верхний график). Далее показаны синтез цифрового частотного фильтра и его амплитудно-частотная характеристика (АЧХ). График АЧХ показан в нижней части рис. 5.10.
На рис. 5.11 показан процесс фильтрации. Он сводится к уточнению модели фильтра (сдвигу АЧХ в область более низких частот и созданию зеркального отражения спектра), проведению прямого преобразования Фурье, выделению фильтром соответствующих составляющих сигнала и, наконец, выполнению обратного преобразования Фурье. Оба преобразования и фильтрация осуществляются в одном выражении (строка с переменной conv). При этом векторы прямых преобразований Фурье для сигнала и для отсчетов частотной характеристики фильтра перемножаются. Обратное преобразование Фурье переводит результат фильтрации во временную область. Полученный в результате фильтрации сигнал практически очищен от шума. Это подтверждает график выходного сигнала, представленный в нижней части рис. 5.11.
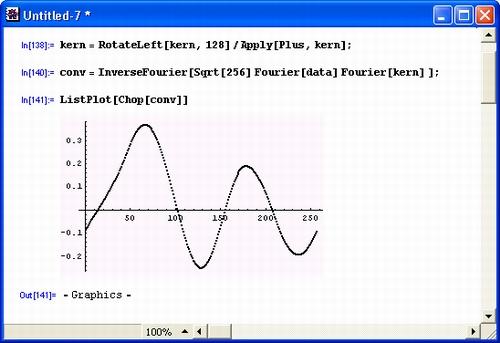
Рис. 5.11. Часть документа, показывающего фильтрацию сигнала и построение графика сигнала, очищенного от шума
Эти примеры показывают высокую эффективность средств Mathematica 3/4 в решении задач спектрального анализа, синтеза сигналов, их фильтрации и иных преобразований. Важно отметить, что в новейшей версии Mathematica 4 использованы ускоренные алгоритмы преобразований Фурье, повышающие скорость выполнения описанных операций в несколько раз. Это открывает возможность решения серьезных задач обработки сигналов, представленных многими тысячами отсчетов. Другими словами – сигналов, реально применяемых в технике связи.
