Преобразования Фурье. Основные понятия о спектральном анализе и синтезе.
На рис. 5.5 показан пример прямого синтеза разнополярных коротких прямоугольных импульсов. Используется известное разложение их в ряд, причем графики построены для 5 и 20 гармоник. Нетрудно заметить, что даже при двадцати гармониках представление такого сигнала гармоническим рядом не очень точно – отчетливо наблюдаются колебания и выбросы, то есть эффект Гиббса.
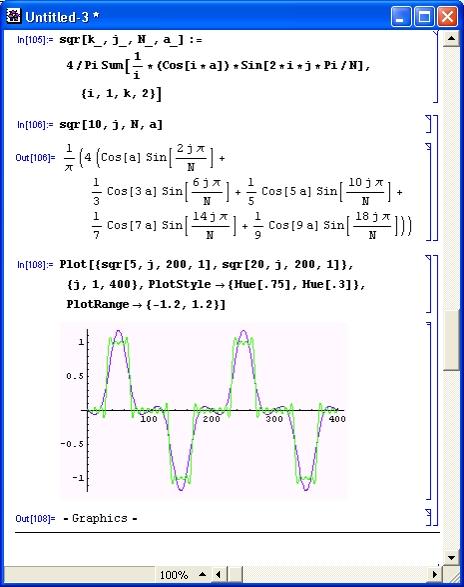
Рис. 5.5. Гармонический синтез коротких разнополярных прямоугольных импульсов
Еще один подобный пример – синтез разнополярных треугольных импульсов – представлен на рис. 5.6. Здесь также используется известное выражение для ряда Фурье. Графики построены для 3 и 20 гармоник. Нетрудно заметить, что гармонический синтез для этого сигнала дает гораздо лучшие результаты – даже три гармоники неплохо воспроизводят сигнал. Это связано с тем, что данный сигнал не имеет разрывов – для него характерны лишь точки резких перегибов временной зависимости.
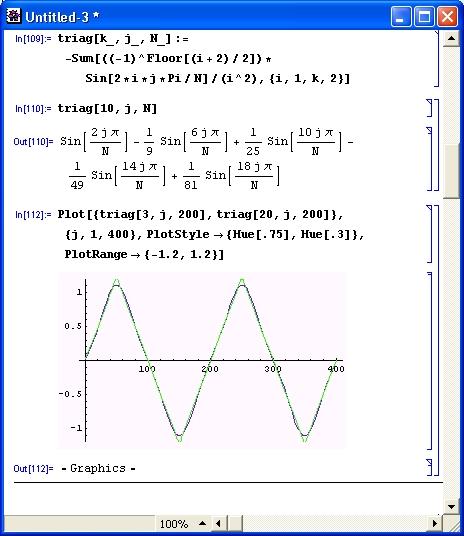
Рис. 5.6. Гармонический синтез симметричных треугольных импульсов
В целом надо отметить, что чем плавнее временная зависимость сигнала, тем меньше проявляются отмеченные выше искажения и слабее заметен эффект Гиббса.
Итак, в результате гармонического анализа сигнала (или его прямого гармонического синтеза) сигнал получается в виде совокупности гармонических сигналов – гармоник. В общем случае каждая гармоника имеет свою амплитуду и фазу, и для их получения в общем случае можно использовать прямое преобразование Фурье (см. ниже).
Полученный спектр сигнала можно подвергать различным преобразованиям, например частотной фильтрации. Полученный после этого измененный спектр гармоник используется (путем гармонического синтеза) для воссоздания искаженного (например, после фильтрации) сигнала.
Простота спектрального подхода обманчива, поскольку он требует довольно громоздких вычислений. Для быстрого их выполнения были созданы различные ускоренные методы спектрального анализа и синтеза – например, метод быстрого преобразования Фурье (БПФ). Но лишь с появлением СКМ класса Mathematica (и ей подобных) спектральный подход превращается в "рабочую лошадку", обеспечивая наглядное и достаточно быстрое решение задач спектрального анализа и синтеза.
