Разложение функций в ряды
Удаление члена с остаточной погрешностью ряда
Из-за особого формата результаты разложения в ряд нельзя явно использовать для расчетов (например, для построения графика функции по данным ее разложения в ряд). Для устранения остаточного члена и получения приемлемых для расчетов выражений можно использовать функции Collect и Normal. Ниже показаны примеры применения этих функций:
Series[Sin[x], {x, 0.7}] x-x3/6+x5/120 -x7/5040+0[X] 8 Collect[%, x] x-x3/6+x5/120 - x7/5040 Normal[Series[Sin[x*y], {x, 0.3}, {y, 0.3}] ] xy-x3 y3/6 f [x_, y ] = xy-x3 y3/6xy-x3 y3/6 f[0.1.0.2] 0.0199987В данном случае результат представлен в формате стандартного вывода. Его можно использовать для создания функций пользователя, например, путем переноса через буфер обмена в правую часть такой функции. Это и показано в конце приведенных выше примеров. Разумеется, можно задать функцию пользователя и напрямую:
F[x_, y_] = Normal [Series [Sin[x* y], {x, 0, 3), {y, 0, 3}] xy-x3 y3/6F[0.1, 0.2] 0.0199987В Mathematica 3/4 преобразование результатов разложения в ряд в стандартные расчетные выражения несколько упрощено. Это позволяет ограничиться описанными выше (но вовсе не единственными) приемами.
Графическая визуализация разложения в ряд
Погрешность разложения в ряд возрастает с ростом отклонения от узловой точки. При больших отклонениях даже качественное описание функции может резко нарушаться – например, монотонно возрастающая функция при вычислении по разложению в ряд может убывать или даже стремиться к бесконечности. Для оценки того, насколько и в какой окрестности исходной точки разложение в ряд адекватно разлагаемой функции, полезно построить на одном рисунке график исходной функции и график выражения, соответствующего полученному ряду (без остаточной погрешности). Другими словами, нужна графическая визуализация разложения в ряд.
Пример графической визуализации разложения в ряд представлен на рис. 5.3. На нем, кстати, использовано описанное выше применение функции Collect для получения результата разложения в обычной форме, допускающей вычисления.
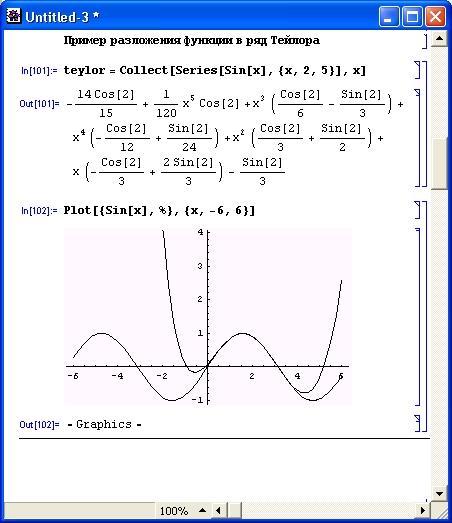
Рис. 5.3. Представление синусоидальной функции рядом Тейлора с графической иллюстрацией его точности
На рис. 5.3 представлены график синусоиды, построенной по аналитическому выражению, и график ее разложения в ряд Тейлора в окрестности точки х 0 =2. Хорошо заметно расхождение за пределами области, примыкающей к оперной точке функции. Как отмечалось, погрешность уменьшается, если х0=0 (ряд Маклорена). К сожалению, при большом числе членов ряда его поведение становится трудно предсказуемым, и погрешность приближения катастрофически нарастает.
