Решение дифференциальных уравнений в численном виде
Многие дифференциальные уравнения не имеют аналитических решений – например, нелинейные. Однако они могут с приемлемой точностью решаться численными методами. Для численного решения систем дифференциальных уравнений используется функция NDSolve:
- NDSolve [eqns, у, {x, xmin, xmax }] – ищет численное решение дифференциальных уравнений .eqns относительно функции у независимой переменной х в интервале от xmin до xmax;
- NDSolve [eqns, {yl, y2,…}, {x, xmin, xmax }] – ищет численные решения относительно функций yi.
MaxSteps – опция к NDSolve, которая определяет максимальное количество шагов.
Часто весьма желательно выводить результаты решения дифференциальных уравнений в графической форме. Рисунок 4.25 поясняет, как это делается при решении системы нелинейных дифференциальных уравнений, описывающих достаточно сложный колебательный процесс.
Нередко решение предпочитают представить на фазовой плоскости. Рисунок 4.26 иллюстрирует такую возможность. Более того, поскольку решается система из трех дифференциальных уравнений, фазовая траектория решения находится в трехмерном пространстве.
Простота задания решения и вывода его результатов в графической форме открывает широкие возможности применения системы для математического моделирования сложных явлений. При этом, в отличие от такого решения с помощью обычных языков высокого уровня (например, Фортран, Бейсик, Паскаль или С), не требуется составления каких-либо программ по реализации численных методов решения систем дифференциальных уравнений, таких как, скажем, метод Рунге-Кутта. Они представлены в виде уже готовых функций.
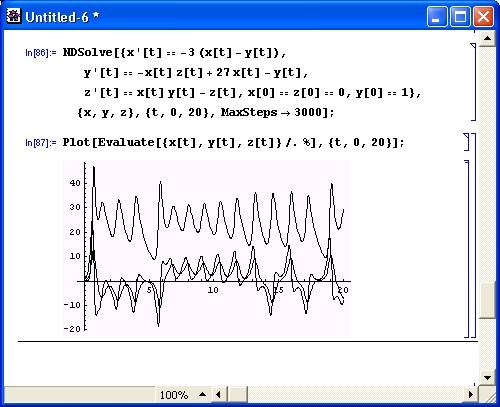
Рис. 4.25. Решение системы дифференциальных уравнений с выводом решения в виде графиков временных зависимостей

Рис. 4.26. Решение системы дифференциальных уравнений с выводом решения в форме кривых на фазовых плоскостях
