Поиск корней уравнений
Для вычисления корней полиномиальных уравнений используется функция Roots:
Roots[lhs == rhs, var]На рисунке 4.18 представлены примеры применения функции Roots.
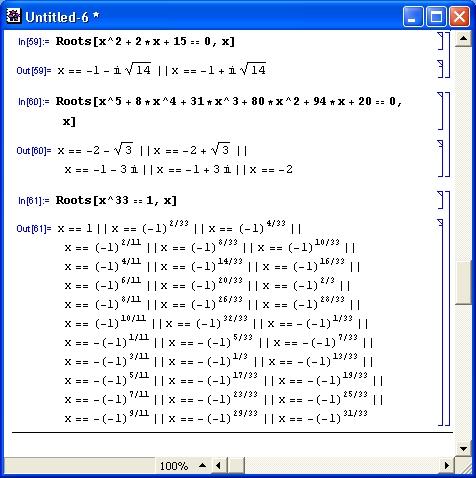
Рис. 4.18. Примеры использования функции Roots
Формат выдачи результатов для функции Roots отличается от такового для функции Solve. Поэтому проверку решения подстановкой надо выполнять как в следующем примере:
e = x ^ 2 + 3x == 23x + x2 == 2N[Roots[e, x]] x == -3.56155 | | x == 0.561553r = {ToRules[ % ]} {{x ^ -3.56155}, {x ^ 0.561553}} e / .r {True, True}Для преобразования результата вычислений в список решений (подобный решениям, получаемым с помощью функции Solve) здесь использована функция ToRules.
При затруднениях в решении уравнений с помощью функции Roots можно использовать следующие опции:
Options[Roots] {Cubics > True, Eliminate > False, EquatedTo > Null, Modulus > 0, Multiplicity > 1, Quar tics > True, Using > True}Ниже они описаны подробно:
- Cubics – указывает, следует ли искать явные решения для неприводимых кубических уравнений;
- EquatedTo – задает выражение для замещения переменной в решении;
- Modulus – задает промежуточную факторизацию полинома;
- Multiplicity– устанавливает кратность каждого из корней в конечном результате;
- Quartics – задает точное решение квадратного уравнения и полинома четвертой степени;
- Using – указывает какие-либо дополнительные уравнения, которые следует использовать для решения уравнений.
Применение опций нередко позволяет получать решения, которые не удаются с первого раза. Однако это требует определенного опыта и понимания сути решаемой задачи.
