Вычисление интегралов. Вычисление интегралов в символьном виде.
Одна из важнейших операций – вычисление первообразных и определенных интегралов в символьном виде. Первообразная – это функция F(x), удовлетворяющая уравнению:
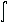f(x)dx = F(x) + C.
Где С – постоянная интегрирования. А вычисление определенного интеграла с пределами – верхним b и нижним а – производится по формуле:
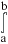f(X)dX = F(b)-F(a).
Заметим, что определенный интеграл может быть представлен как аналитическим, так " численным значением. Для вычисления численных значений определенных интегралов разработан ряд приближенных методов – от простых (прямоугольников и трапеций) до сложных, автоматически адаптирующихся к характеру изменения подынтегральной функции f(x).
Для интегрирования в системе Mathematica используются следующие функции:
- Integrate [f, x] – возвращает первообразную (неопределенный интеграл) подынтегральной функции f по переменной х;
- Integrate [f, {x, xmin, xmax}] – возвращает значение определенного интеграла с пределами от x min до x max ;
- Integrate [f, {x, xmin, xmax}, {у, ymin, ymax},…] – возвращает значение кратного интеграла с пределами от x min до x max по переменной х, от y min до y max по переменной у и т. д. (кратность реально не ограничена).
Обычно функция Integrate применяется в простейшей форме, но она имеет три характерные опции:
Options[Integrate] {Assumptions > {}, GenerateConditions > Automatic, PrincipalValue > False)Для обозначения бесконечных пределов используется константа Infinity. Эта константа означает положительную бесконечность, для задания отрицательной бесконечности она используется со знаком "минус". Пределы могут задаваться как константами, так и функциями.
Особый интерес, естественно, вызывает применение функции Integrate для вычисления заданных пользователем неопределенных интегралов в символьном виде. Это иллюстрируют примеры на вычисление неопределенных интегралов с алгебраическими подынтегральными функциями, представленные на рис. 4.2.
Рис. 4.2. Примеры вычисления неопределенных интегралов (начало)