Вычисление производных
Следующие примеры иллюстрируют вычисление производных от первого до третьего порядка включительно для функции f [ х ], заданной пользователем.
| Ввод (In) | Вывод (Out) |
|---|---|
| f[x]: = х/(1+х^ 2) | |
| D[f[x],{x,l}] | -2x2 /(1+x2)2 +1/(1+x2) |
| D[%,x] | -8x3 /(1+x2)3 +6x/(1+x2)2 |
| D[f[x],{x,2}] | -8x3 /(1+x2)3 +6x/(1+x2)2 |
| D[D[D[f[x],x],x],x] | -48x4 /(1+x2)4 +48x2 /(1+x2)3-6/(1+x 2)2 |
| D[f[x],{x,3}] | -48x4 /(1+x2)4 +48x2 /(1+x2)3-6/(1+x 2)2 |
Из предпоследнего примера видно, что для вычисления высших производных возможно последовательное применение функции D.
На рис. 4.1 показано построение графика функции Sin [x] /х, заданной как функция пользователя, и ее производной с помощью функции Plot.
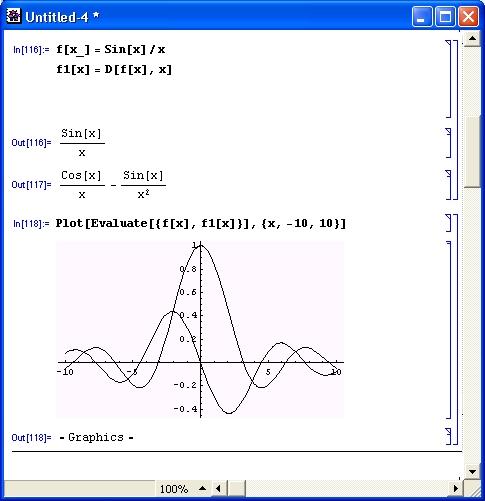
Рис. 4.1. График функции Sin[x]/x и ее производной
В целом средства для символьного вычисления производных, имеющиеся в ядре системы Mathematica, охватывают практически все важные типы математических выражений. Они могут включать в себя как элементарные, так и специальные математические функции, что выгодно отличает систему Mathematica от некоторых простых систем символьной математики, таких как Derive.
Использование функции Dt демонстрируют примеры, приведенные ниже.
| Ввод (In) | Вывод (Out) |
|---|---|
| Dt[x*n,x] | xn (n/x +Dt[n, x] Log[x]) |
| Dt[x*Sin[x],x] | xCos[x] + Sin[x] |
| Dt[Exp[x/b],x] | ex/b /b(1/b-xDt[b, x]/b2) |
| Dt[a*x^ 2+b*x+c,x] | b+ 2 ax + x2 Dt[a, x] + xDt[b, x] + Dt[c, x] |
| Dt[x*n,{x,2}] | xn (n/x+Dt[n, x] Log[x]) + xn (-n/x2 2Dt[n, x] +Dt[n, {x/2}]Log[x]) |
| Dt[Log[3*x/4],x] | 1/x |
| Dt[BesselJ[2,x],x] | 1/2(BesselJ[l, x] – BesselJ[3, x]) |
| Dt[ChebyshevT[4,x],x] | -16x + 32x3 |
Обратите внимание на то, что порой результаты для одного и того же дифференцируемого выражения у функций D и Dt заметно различаются. Это вполне закономерно вытекает из различных определений данных функций.
