Вычисление кратных интегралов
Mathematica способна вычислять даже кратные интегралы с фиксированными и переменными верхним или нижним пределами. Кратный, например двойной, интеграл с фиксированными пределами имеет вид:
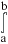
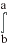f(x,y)dxdy.
На рис. 4.7 представлено вычисление нескольких двойных определенных интегралов.
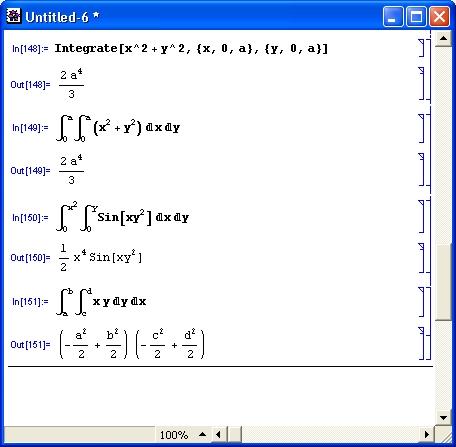
Рис. 4.7. Примеры вычисления двойных определенных интегралов
Следующий пример при двух форматах ввода показывает вычисление двойного неопределенного интеграла двойным применением функции Integrate:
Integrate!Integrate[x ^ 3 + y ^ 3, x], y] x4y / 4 + y4x / 4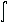
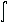( (x3 + y3) dx) dy.
x4y / 4 + y4x / 4Другая серия примеров (рис. 4.8) показывает, как вычисляются двойные и тройные интегралы, пределы которых сами по себе являются функциями.
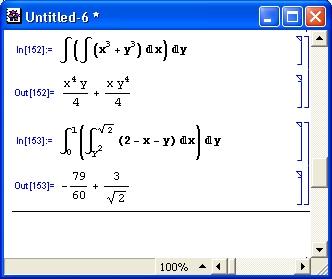
Рис. 4.8. Примеры вычисления кратных интегралов с пределами-функциями
Хотя вычисление двойного интеграла предусмотрено в синтаксисе функции Integrate, это не всегда дает результат. Как правило, вычисление кратных интегралов лучше производить, используя последовательное вычисление однократных интегралов, вложенных друг в друга. Это и показывают приведенные примеры.