Дополнительные функции для решения уравнений
Имеется также ряд дополнительных функций, которые используются описанными ранее функциями и также могут применяться при решении нелинейных уравнений:
- Auxiliary [v] – применяется модулем Solve для указания того, что переменная v должна использоваться функцией Roots для результирующих решений, но соответствующие значения v не должны быть включены в окончательный ответ;
- Eliminate [eqns, vars] – исключает переменные vars из системы уравнений eqns;
- FindRoot [Ihs == rhs, {x, x0}] – ищет численное решение уравнения Ihs == rhs, начиная с х = x0;
- MainSolve [eqns] – основная функция для преобразования системы уравнений. Ее вызывают Solve и Eliminate. Уравнения должны быть представлены в форме Ihs == rhs. Они могут объединяться с помощью && и | |. MainSolve возвращает False, если не существует решения уравнений, и возвращает True, если все значения переменных являются решениями. MainSolve перестраивает уравнения, применяя определенные директивы;
- MainSolve [eqns, vars, elim, rest] – пытается перестраивать уравнения eqns так, чтобы найти решения для переменных vars и исключить переменные elim. Список rest может включаться для указания порядка исключения любых остальных переменных;
- NRoots [lhs==rhs, var] – возвращает список численных приближений корней полиномиального уравнения;
- Residue [ехрr, {х, х0 } ] – ищет вычет ехрг в точке х = х0;
- SolveAlways [eqns, vars] – возвращает значения параметров, которые превращают уравнения eqns в тождества для всех значений переменных vars.
Примеры использования некоторых из этих функций показаны на рис. 4.19.
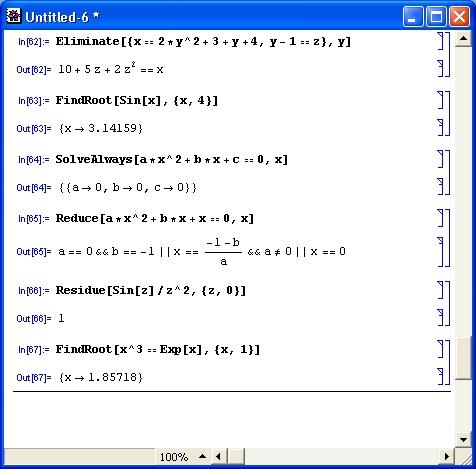
Рис. 4.19. Примеры применения дополнительных функций для решения уравнений
В целом надо отметить, что система Mathematica обладает обширными средствами для решения уравнений и их систем. Умение их применять – залог правильного и эффективного решения сложных математических задач, относящихся к классу решения уравнений.
