Разложение функций в ряды
Представление и обработка данных – еще один класс математических задач, имеющих явно практическую направленность. В этом уроке мы рассмотрим ряд средств решения этих задач – начиная с общеизвестного разложения аналитических функций в ряды Тейлора и Маклорена и кончая различными видами аппроксимации, интерполяции и регрессии. Будут также затронуты прикладные вопросы применения интерполяции при спектральном анализе сигналов и моделировании нелинейных электрических и электронных цепей.
Разложение функций в ряды Тейлора и Маклорена
Одна из широко распространенных математических задач представления данных – разложение заданной аналитической функции в степенной ряд Тейлора относительно некоторой узловой точки с абсциссой хО. Такой ряд нередко проще самой функции (в том смысле, что не требует вычисления даже элементарных функций и вычисляется с помощью только арифметических операций) и дает единообразное представление для разлагаемых функций в виде обычных степенных многочленов.
Большинство достаточно гладких функций, не имеющих разрывов в области разложения, довольно точно воспроизводятся рядом Тейлора. Как правило, такие разложения достаточно просты в окрестностях узловой точки разложения.
Для разложения в ряд используются следующие функции системы Mathematical:
- Series[f, {х, х0, п}] – выполняет разложение в степенной ряд функции f в окрестности точки х=х0 по степеням (х-х0)^ n;
- Series [f, {х, х0, nх}, {у, у0, nу}] – последовательно ищет разложения в ряд сначала по переменной у, затем по х;
- SeriesCoef ficient [s,n] – возвращает коэффициент при переменной n-й степени ряда s;
- SeriesData [х, х0, {а0, al,…}, nmin, nmax, den] – представляет степенной ряд от переменной х в окрестности точки х0. Величины ai являются коэффициентами степенного ряда. Показатели степеней (х-х0) представлены величинами nmin/den, (nmin+1) /den,…, nmax/den.
Суть разложения функции в степенной ряд хорошо видна из разложения обобщенной функции/(д:), представленного на рис. 5.1 (выходные ячейки имеют стандартный формат).
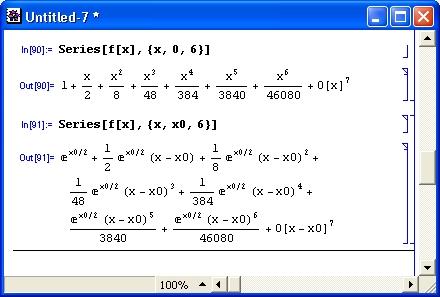
Рис. 5.1. Разложение в ряд обобщенной функции f(x)
В первом примере разложение идет относительно исходной точки х0=0, что соответствует упрощенному ряду Тейлора, часто называемому рядом Маклорена. Во втором случае разложение идет относительно исходной точки х0, отличной от нуля. Обычно такое разложение сложнее и дает большую остаточную погрешность.
В соответствии с принятой математической символикой эта погрешность обозначается как О [x]i с показателем степени, указывающим на порядок погрешности. Следует отметить, что разложение в ряд использует особый формат вывода, частью которого и является член остаточной погрешности. На рис. 5.2 показано разложение в ряд Тейлора для нескольких функций, причем вывод дан в стандартной форме.

Рис. 5.2. Примеры представления функций рядами
Нетрудно заметить, что не все функции разлагаются в ряд Тейлора системой. Mathematica. Например, не имеют разложения логарифм и квадратный корень – они возвращаются в исходном виде. А разложение факториала представлено через гамма- и полигамма-функции.
