Интерполяция, аппроксимация и регрессия
Нередко исходные данные при решении математических задач представлены рядом точек произвольной зависимости вида у(х). Сама по себе эта зависимость может быть неизвестной. Для вычисления промежуточных значений функции используется аппарат интерполяции. При нем истинная функция заменяется аппроксимирующей функцией, которая в узловых точках дает точные значения ординат и позволяет вычислить значения интерполируемой функции в промежуточных точках.
Полиномиальная интерполяция и аппроксимация
Для решения задач интерполяции и аппроксимации функций, заданных рядом узловых точек, в Mathematica используются следующие функции:
- InterpolatingFunctionfrange, table[ ] – возвращает интерполирующую функцию, позволяющую вычислять промежуточные значения в заданном диапазоне range для таблицы table;
- InterpolatingPolynomial [data, var] – возвращает полином (степенной многочлен) по переменной var, значения которого в узловых точках точно совпадают с данными из списка data. Он может иметь форму { {xl, f1}, {х2, f2},…} или {fl, f2,…} (во втором случае xi принимают значения 1, 2,…). Вместо fi может быть список {fi, dfi, ddfi,…}, указывающий значения производных в точках xi;
- Interpolation [data] – конструирует объект InterpolatingFunction.
InterpolationOrder – опция функции Interpolation, указывающая степень подходящего полинома. При ее значении, равном 1, осуществляется кусочно-линейная интерполяция. Целое значение, большее единицы, задает степень глобальной полиномиальной интерполяции.
Применение основной функции Interpolation поясняет следующий пример:
data = Table[{x, x^2 + 1}, {x, 1, 5}] {{1, 2}, {2, 5}, {3, 10}, {4, 17}, {5, 26}} funi = Interpolation[data] InterpolatingFunctionf{{1, 5}}, 0] {funi [1.5], funi[3], funi[4.5]} {3.25, 10, 21.25}Таким образом, на заданном отрезке изменения х функция Interpolation позволяет найти любое промежуточное значение функции funi [x], в том числе значения в узловых точках.
Теперь рассмотрим часто используемую полиномиальную аппроксимацию, при которой ищется полином, график которого точно проходит через узловые точки данных.
Степень интерполирующего (и аппроксимирующего) полинома всегда на 1 меньше числа узловых точек интерполяции или аппроксимации. Аппроксимация отличается от интерполяции тем, что предполагает получение аппроксимирующей функции в явном виде. При полиномиальной аппроксимации такой функцией является степенной многочлен.
Пример на рис. 5.13 иллюстрирует технику проведения полиномиальной аппроксимации с применением интерполирующего степенного многочлена.
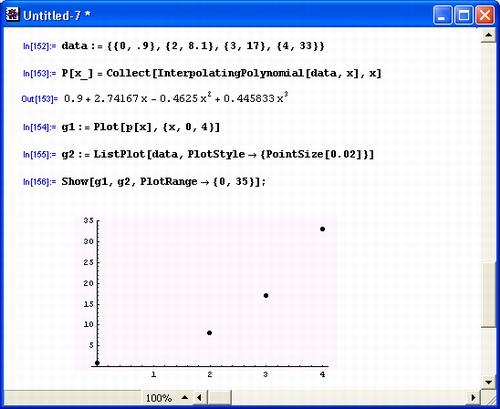
Рис. 5.13. Полиномиальная аппроксимация таблично заданных данных
Как и следовало ожидать, степень аппроксимирующего многочлена оказалась равной трем, поскольку было задано четыре пары данных. На рис. 5.13 представлено также сравнение результата полиномиальной аппроксимации с исходными данными. Исходные данные представлены на графике в виде точек, а зависимость, представленная аппроксимирующим полиномом, выведена сплошной линией.
В узлах интерполяции значения интерполирующего многочлена точно совпадают со значениями исходных данных. Однако это не гарантирует малую погрешность за пределами узловых точек (особенно при экстраполяции функций). Чем больше пар данных и чем выше степень аппроксимирующего многочлена, тем выше погрешность аппроксимации. Обычно аппроксимация при степени многочлена выше 8-10 не применяется из-за резкого возрастания погрешности. При большом числе пар исходных данных более полезной на практике является регрессия.
