Ортогональные многочлены
Специальные математические функции являются решениями линейных дифференциальных уравнений специального вида или представлениями особых интегралов, которые не могут быть выражены через элементарные функции. Здесь не приводятся определения специальных математических функций ввиду их общеизвестности и наличия соответствующей информации в справочной базе данных систем Mathematica.
К сожалению, входной язык общения с системами Mathematica 3/4 не предусматривает использования греческих букв для имен специальных функций (хотя палитра с такими буквами есть), и их имена задаются английскими словами. Специальные математические функции удобно подразделять на несколько групп, представленных ниже.
Одними из широко распространенных специальных функций являются ортогональные многочлены (полиномы). Mathematica имеет следующие функции, возвращающие значения ортогональных многочленов:
- ChebyshevT [n, х] – полином Чебышева n-й степени первого рода;
- CyebyshevU [n, x] – полином Чебышева n-й степени второго рода;
- HermiteH[n, х] – полином Эрмита n-й степени;
- JacobiP[n, a, b, х] – полином Якоби n-й степени;
- GegenbauerC [n, m, х] – полином Гегенбауэра;
- LaguerreL[n, х] – полином Лагерра n-й степени;
- LaguerreL[n, а, х] – обобщенный полином Лагерра n-й степени;
- LegendreP [n, х] – полином Лежандра n-й степени;
- LegendreP [n, m, x] – присоединенный полином Лежандра;
- LegendreQ [n, z] – функция Лежандра второго рода n-го порядка;
- LegendreQ [n, m, z] – присоединенная функция Лежандра второго рода.
LegendreType – опция для функций LegendreP и LegendreQ; она указывает выборы разрывов кривой для функций Лежандра на комплексной плоскости.
Все ортогональные полиномы имеют простые рекуррентные представления. Поэтому приведенные выше функции вычисляются по ним довольно быстро и точно. Они находят широкое применение в технике интерполяции и аппроксимации функций.
Следующие примеры иллюстрируют работу с ортогональными многочленами.
| Ввод (In) | Вывод (Out) |
|---|---|
| ChebyshevT [ 8, х] | 1-32 x2 + 160 x4 – 256 x6 + 128 x8 |
| ChebyshevT [5, 0.2] | 0.84512 |
| ChebyshevU [3.0. 15] | -0.573 |
| HermiteH[4.3] | 876 |
| JacobiP[3,l,2.0.2] | -0.256 |
| GegenbauerC [ 3, 1, x] | -4 x + 8 x3 |
| N [LaguerreL [3,x]] | 0.166667 (6. – 18 .x+ 9 .x2 – 1. X3) |
| LegendreP [ 5, x ] | 15 x /6-35 x3 /4+63 x5 /8 |
| LegendreQ[2.0.2] | -0.389202 |
Важно отметить, что при указании конкретного значения параметра п и символьном значении параметра х функции этой группы возвращают присущие им представления через степенные многочлены с соответствующими коэффициентами.
На рис. 6.1 показаны графики ортогональных полиномов Чебышева ChebyshevT и ChebyshevU. Для этих полиномов характерно изменение от -1 до +1 при \х\<1, причем при высоком порядке полиномов графики функций имеют колебательный характер.
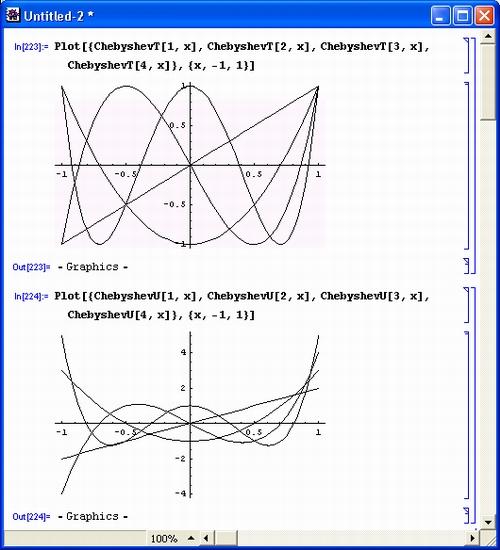
Рис. 6.1. Графики ортогональных полиномов Чебышева ChebyshevT (сверху) и ChebyshevU (снизу)
