Интегральные показательные и родственные им функции
К другой известной группе специальных функций относятся интегральные показательные и родственные им функции:
- Coshlntegralfx] – гиперболический интегральный косинус;
- Coslntegral [х] – интегральный косинус С1(х);
- Erf [z] – функция ошибок (интеграл вероятности);
- Erf[z0, zl] – обобщенная функция ошибок erf (zl)-erf (z0);
- Erf с [z] – дополняющая функция ошибок 1-erf (z);
- Erfi [z] – мнимое значение функции ошибок erf (iz) /i;
- ExplntegralE [n, z] – интегральная показательная функция Е(п,z);
- ExplntegralEi[z] – интегральная показательная функция Ei(z);
- Loglntegral [z] – интегральный логарифм li(z);
- Sinhlntegral [x] – интегральный гиперболический синус;
- Sinlntegral [х] – интегральный синус 81(лг).
Ниже представлены примеры применения этих функций.
| Ввод (In) | Вывод (Out) |
|---|---|
| Coshlntegral[1.] | 0.837867 |
| Coslntegral [1. ] | 0.337404 |
| Erf[l.] | 0.842701 |
| Erf [2. +1*3.] | -20.8295 + 8.68732 I |
| Erf[2.,3.] | 0.00465564 |
| Erfc[l.] | 0.157299 |
| Erfi[l.] | 1.65043 |
| ExplntegralE [3.1.] | 0.109692 |
| ExpIntegralEi [1. ] | 1.89512 |
| Loglntegral [2. +3. *I ] | 2.3374 + 2.51301 I |
| Sinhlntegral [1. ] | 1.05725 |
| Sinlntegral [1. ] | 0.946083 |
На рис. 6.4 представлены графики ряда интегральных показательных функций, дающие представление об их поведении при вещественном аргументе.
Следует обратить внимание на то, что большая часть этих функций может иметь комплексный аргумент. Для получения численных значений функций нужно задавать аргумент в форме вещественного числа или комплексного числа с вещественными действительной и мнимой частями.
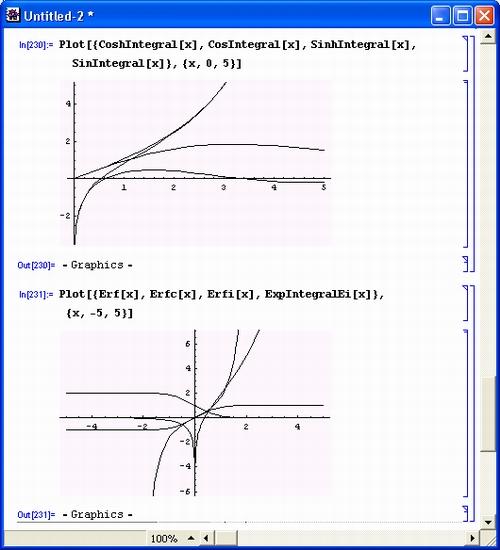
Рис. 6.4. Графики интегральных показательных функций
