Эллиптические интегралы и интегральные функции
В ядро системы Mathematica входят эллиптические функции и функции вычисления эллиптических интегралов:
- EllipticE [m] – полный эллиптический интеграл Е(т);
- EllipticE [phi, m] – эллиптический интеграл второго рода Е(Ф\т);
- EllipticExp [u, {a, b}] – обобщенный экспоненциал, связанный с эллиптической кривой у2 = х3 + ах2 + bx,
- EllipticExpPrime [и, {а, b}] – производная по первому аргументу EllipticExp[u, {a, b}];
- Elliptic? [phi, m] – эллиптический интеграл первого рода Р(Ф\т);
- EllipticK[m] – полный эллиптический интеграл первого рода К(т)\
- EllipticLog [ {х, у}, {а, b}] – обобщенный логарифм, связанный ц эллиптической кривой у2 = n3 + а х2 + b т,
- EllipticNomeQ [m] – возвращает значение q = Exp[-PiEllipticK[l – m]/EllipticK[m]];
- Elliptic?! [n, phi, m] – эллиптический интеграл третьего рода П(и; Ф\т);
- Elliptic?! [n, m] – полный эллиптический интеграл П(п|т);
- EllipticTheta [i, z, q] – эллиптическая тета-функция &.(z, q), где i = 1, 2, 3 или 4;
- EllipticThetaC [u, m] – эллиптическая тета-функция Невилла $ с (и, т);
- EllipticThetaD [u, m] – эллиптическая тета-функция Невилла $ d (u, m);
- EllipticThetaN [u, m] – эллиптическая тета-функция Невилла $ п (и,m);
- EllipticThetaPrime [i, z, q] – производная по второму аргументу эллиптической тета-функции в. (z, q), где i= 1, 2, 3 или 4;
- EllipticThetaS [u, m] – эллиптическая тета-функция Невилла u s (w, т);
- FresnelCfx] – интеграл Френеля С(х),
- FresnelS[x] – интеграл Френеля S(x);
- InverseJacobi** [v, m] – обратная эллиптическая функция Якоби с обобщенным названием **. Возможны следующие наименования для **: CD, CN, CS, DC, DN, DS, NC, ND, NS, SC, SD И SN;
- JacobiAmplitude [u, m] – амплитуда для эллиптических функций Якоби;
- Jacobian – опция для FindRoot; может применяться для указания якобиана системы функций, для которых ищется корень;
- Jacob!** [u, m] – эллиптическая функция Якоби с обобщенным именем **, которое может принимать значения CD, CN, CS, DC, DN, DS, NC, ND, NS, SC, SD и SN;
- JacobiSymbol [n, m] – символ Якоби от n и in;
- JacobiZeta [phi, m] – дзета-функция Якоби Z(Ф|m);
- WeierstrassP [u, g2, g3] – эллиптическая функция Вейерштрасса Р,
- WeierstrassPPrime [u, g2, g3] – производная эллиптической функции Вейерштрасса Р'nо переменной и.
Приведем примеры использования некоторых из этих функций.
| Ввод (In) | Вывод (Out) |
|---|---|
| EllipticE[0.1] | 1.53076 |
| EllipticE[Pi,0.1] | 3.06152 |
| EllipticF [Pi/2.0.1] | 1.61244 |
| EllipticPi[Pi,0.1] | -0.0266412-1.09088 I |
| EllipticK[0.l] | 1.61244 |
| FresnelC[1.0] | 0.779893 |
| FresnelSfl.0] | 0.438259 |
| JacobiCD[l,0.2] | 0.605887 |
| JacobiZeta [ Pi, 0. 5] | 0 |
| WeierstrassPPrime [1.,2.,3.] | -1.31741 |
Эллиптические функции (интегралы) широко используются в оптических расчетах и в астрофизике. На рис. 6.9 показаны графики некоторых эллиптических функций.
Рисунок 6.10 показывает построение контурного графика на комплексной плоскости с параметрическим заданием функций, выраженных через функцию Якоби и эллиптические интегралы. Нетрудно заметить, что график описывает довольно сложную и специфическую поверхность, содержащую периодические пики и впадины.
Читателю рекомендуется просмотреть ряд других примеров на использование функций данного раздела (например, в справочной базе данных системы Mathematica).
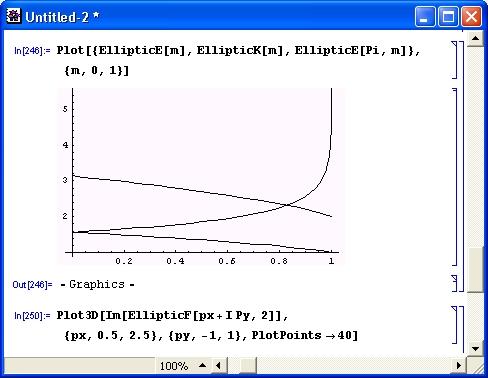
Рис. 6.9. Графики некоторых эллиптических функций
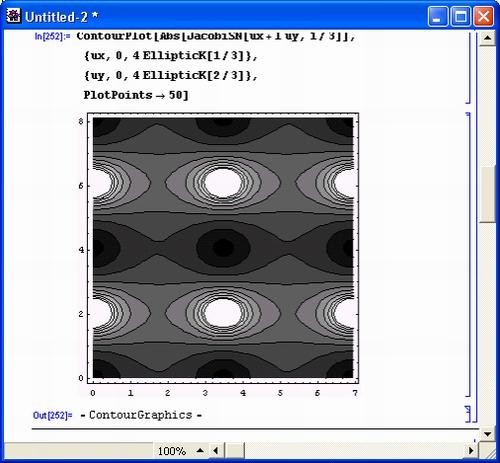
Рис. 6.10. Контурный график с параметрическим заданием комбинированной функции, содержащей функцию Якоби и эллиптические интегралы
