Гамма- и полигамма-функции
Широко используются гамма-функция и относящиеся к ней родственные функции:
- Gamma [ а ] – эйлерова гамма-функция;
- Gamma [ a, z] – неполная гамма-функция;
- Gamma [a, z 0, z 1 ] – обобщенная неполная гамма-функция Gamma (а, z 0) – Gamma(a,zl);
- GammaRegularized [a, z] – регуляризованная неполная гамма-функция (а,2)=Gamma(а,z)/Gamma(a);
- GammaRegularized[a, z0, zl] – обобщенная неполная гамма-функция Q(a,z0)-Q(a, zl);
- LogGamma [ z ] – логарифм эйлеровой гамма-функции;
- PolуGamma [ z ] – дигамма-функция \|/(z);
- PolуGamma [n, z] – n-я производная от дигамма-функции.
Приведем примеры вычисления этих функций.
| Ввод (In) | Вывод (Out) |
|---|---|
| Gamma[l,2.+3.*I] | -0.133981-0,.0190985 I |
| Gamma [0.5] | 1.77245 |
| Gaitima [1.2., 3. ] | 0.0855482 |
| GammaRegularized [ 1, 2. +3. I, 4. +6. *I ] | -0.139176-0.0366618 I |
| LogGamma [0.5] | 0.572365 |
| LogGarama [ 2. +3. * I ] | -2.09285 + 2.3024 I |
| PolyGamma[l] | -EulerGamma |
| PolyGamma [ 1. ] | -0.577216 |
| PolyGarama [2. +3. *I] | 1.20798 + 1.10413 I |
Как видно из этих примеров, данный класс функций (как и многие другие) определен в общем случае для комплексного значения аргумента.
На рис. 6.5 представлены графики эйлеровой гамма-функции и неполной гамма-функции при вещественном аргументе. Поведение эйлеровой гамма-функции довольно сложно, особенно при отрицательных значениях аргумента – наблюдаются характерные разрывы функции с ее уходом в положительную и отрицательную бесконечность.
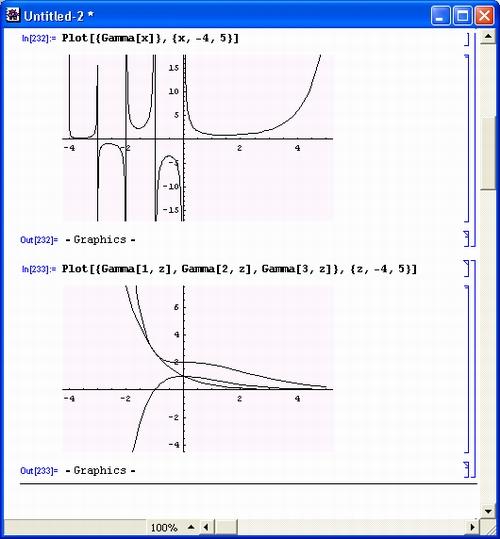
Рис. 6.5. Графики эйлеровой гамма-функции (сверху) и неполной гамма-функции (снизу)
Поведение эйлеровой гамма-функции в комплексной плоскости довольно интересно. На рис. 6.6 показан контурный график этой функции, отражающий ее поведение на комплексной плоскости в ограниченной области изменения действительной и мнимой частей аргумента.
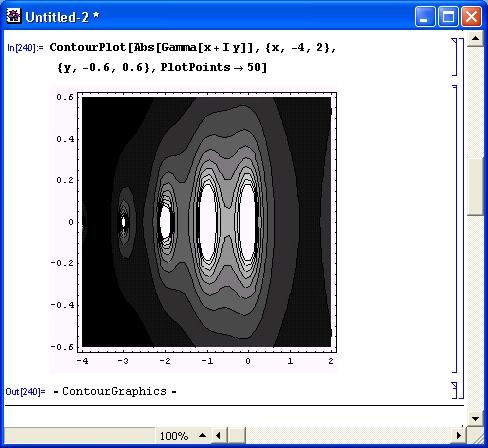
Рис. 6.6. Контурный график эйлеровой гамма-функции на комплексной плоскости
Графики других гамма-функций пользователь может' построить и просмотреть самостоятельно.
