Сглаживание данных (DataSmoothing)
В подпакете DataSmoothing определены функции для сглаживания данных, имеющих большой случайный разброс. К таким данным обычно относятся результаты ряда физических экспериментов, например по энергии элементарных частиц, или сигналы, поступающие из космоса. Для того чтобы отсеять информацию из таких данных с большим уровнем шумов и применяется процедура сглаживания. Она может быть линейной (например, усреднение по ряду точек) или нелинейной.
Определены следующие функции сглаживания:
- MovingAverage [data, r] – сглаживание данных data методом усреднения для г точек;
- MovingMedian [data, r] – сглаживание данных data по медиане для г точек (опция RepeatedSmoothing › True используется для повторного сглаживания);
- LinearFilter [data, {c0, c1,…, сr-j} ] – линейная фильтрация (сj– весовые множители);
- ExponentialSmoothing [data, a] – экспоненциальное (нелинейное) сглаживание, параметр а задает степень сглаживания.
Ниже представлены результаты сглаживания символьных данных, выявляющие соотношения, используемые при сглаживании:
ds: = {x1, x2, x3, x4, x5} MovingAverage[ds,3] {1/3* (x1 + x2 + x3), - (x2 + x3 + x4), - (x3 + x4 + x5)} MovingMedian[ds,3] {x2, x3, x4} ExponentialSmoothing[ds, 0.2] {x1, x1 + 0.2 (-x1 + x2), x1+0.2 (-x1 + x2) +0.2 (-x1-0.2 (-x1 + x2) + x3), x1+0.2(-x1+x2)+0.2 (-x1-0.2 (-x1 + x2) +x3) +0.2 (-x1-0.2 (-x1+x2) - 0.2 (-x1-0.2 (-x1 + x2) + x3) + x4), x1+0.2(-x1 + x2) +0.2(-x1-0.2(-x1 + x2) +x3) + 0.2 (-x1-0.2 (-x1+x2) - 0.2(-x1-0.2(-x1 + x2) + x3) + x4) + 0.2 (-x1-0.2 (-x1+x2) - 0.2 (-x1-0.2 (-x1+x2) + x3) -0.2 (-x1-0.2 (-x1+x2) - 0.2 (-x1-0.2 (-x1 + x2) + x3) + x4) + x5)}Применение сглаживания усреднением иллюстрирует рис. 12.2. На нем задан массив (таблица) из 500 случайных точек с равномерным распределением и создан графический объект из этих точек в виде кружков малого диаметра. Затем выполнена операция сглаживания (по 12 смежным точкам) и создан графический объект сглаженных точек в виде кружков большего диаметра. Для сопоставления оба объекта построены на одном графике функцией Show.
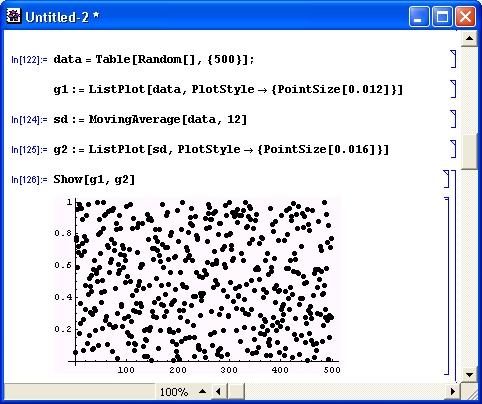
Рис. 12.2. Пример линейного сглаживания данных из 500 точек
Нетрудно заметить, что сглаженные точки группируются вокруг среднего значения, равного 0.5, тогда как исходные точки разбросаны практически равномерно по всему полю рисунка. Эффективность нелинейного (экспоненциального) сглаживания демонстрирует рис. 12.3. Показанный на этом рисунке документ построен по тому же принципу, что и документ рис. 12.2.
Остальные функции сглаживания можно использовать аналогичным образом. Выбор метода сглаживания зависит от решаемых пользователем задач и остается за ним.
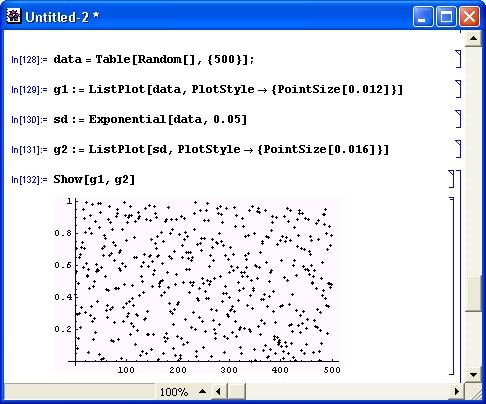
Рис. 12.3. Пример экспоненциального сглаживания
