Сплайн-регрессия (SplineFit)
Сплайны представляют собой набор полиномов невысокой степени, последовательно применяемых к наборам точек аппроксимирующей функции. Чаще всего используется кубическая сплайновая аппроксимация, при которой коэффициенты полиномов выбираются из условий равенства в стыкуемых точках не только значений функции, но также первой и второй производных. Это придает графику сплайна вид плавной кривой, точно проходящей через узловые точки и напоминающей изгибы гибкой линейки (spline в переводе – гибкая линейка).
Подпакет SplineFit пакета NumericalMath содержит функцию для проведения сплайн-регрессии, при которой сплайн-функция проходит максимально близко к аппроксимируемым точкам в смысле наилучшего среднеквадратичного приближения. Для этого используется функция SplineFit [data, type], которая возвращает сплайн функцию для данных data, используя сплайн-аппроксимацию типа type – по умолчанию это кубический сплайн Cube (другие типы – Bezier и CompositeBezier).
Рисунок 12.9 показывает пример сплайн-регрессии для обычной зависимости у(х), представленной пятью парами точек. На нем построены также графики аппроксимирующей функции и исходных точек.
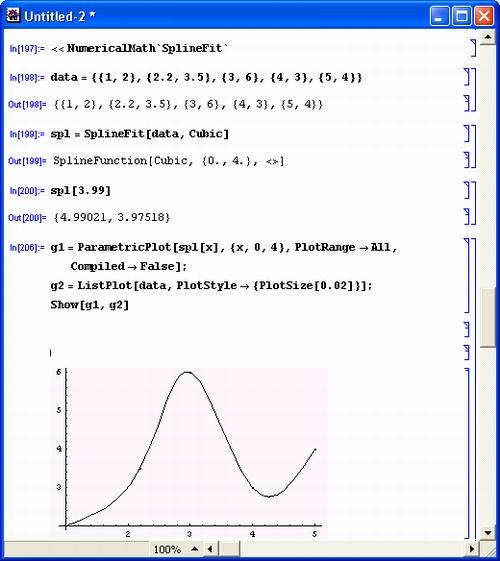
Рис. 12.9. Пример сплайн-регрессии для зависимости у(х), заданной списком координат своих узловых точек

Рис. 12.10. Пример сплайн-интерполяции параметрически заданной функции
Специфика сплайн-регрессии по функции SplineFit заключается в преобразовании значений как xi, так и yi. Это позволяет представлять сплайнами в общем виде параметрически заданные функции, что поясняет рис. 12.10.
