Регрессия. Линейная регрессия общего вида (LinearRegression).
В подпакете LinearRegression имеются расширенные функции для проведения линейной регрессии общего вида – в дополнение к включенной в ядро функции Fit. Прежде всего это функция Regress:
- Regress [data, { I, х, х^2 }, х] – осуществляет регрессию данных data, используя квадратичную модель;
- Regress [data, {I, x1, x2, xlx2 }, {x1, x2 }] – осуществляет регрессию, используя в ходе итераций зависимость между переменными x 1 и х 2 ;
- Regress [data, {f 1, f2,…}, vars] – осуществляет регрессию, используя модель линейной регрессии общего вида с уравнением регрессии, представляющим линейную комбинацию функций f i от переменных vars.
Данные могут быть представлены списком ординат {у1,у2,…} или списком:
{{x11,x12,...,y1}, {x21,x22,...,y2},...}Ниже приведены примеры использования функции Regress:
<< Statistics`LinearRegression` data={{1.1.9},{2.2.95},{3.4.3},{4.4.8},{5.5}} {{1, 1.9}, {2, 2.95}, {3, 4.3}, {4, 4.8}, (5, 5}} (regress = Regress[data, {l,x, x^2}, x] Chop[regress, 10^(-6)]) [Parameter-Table >| Estimate | SE | TStat | PValue | |
| 1 | 0.1 | 0.421613 | 0.237185 | 0.834595 |
| x | 1.89786 | 0.321297 | 5.90687 | 0.0274845' |
| X2 | -0.182143 | 0.0525376 | -3.4669 | 0.0740731 |
RSquared > 0.988994, AdjustedRSquared > 0.977988, EstimatedVariance > 0.0386429, ANOVATable >| DF | SumOfSq | MeanSq | FRatio | PValue | |
| Model | 2 | 6.94471 | 3.47236 | 89.8577 | 0.0110062, |
| Error | 2 | 0.0772857 | 0.0386429 | ||
| Total | 4 | 7.022 |
func = Fit[data, {l,x,.x^2}, x] 0.1 +1.89786x-0.182143x2Options[Regress] {RegressionReport > SurnmaryReport, IncludeConstant > True, BasisNames > Automatic, Weights > Automatic, Tolerance > Automatic, ConfidenceLevel > 0.95}На рис. 12.6 показан еще один пример проведения регрессии, сопровождаемой графической визуализацией с помощью функции MultipleListPlot.
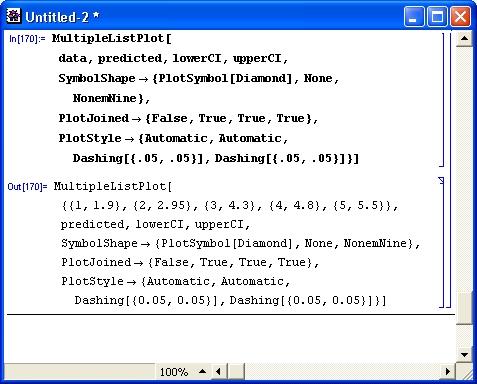
Рис. 12.6. Пример проведения регрессии с графической визуализацией
Пакет линейной регрессии содержит и ряд иных функций, с которыми можно ознакомиться с помощью справочной базы данных системы Mathematica. Напоминаем еще раз, что сама функция при линейной регрессии может быть нелинейна, она является линейной только относительно искомых коэффициентов регрессии.
