Разложение функций в ряд Фурье
Чтобы упростить полученное выражение, ядру Maple нужно сообщить, что m является целым числом. Для этого вводим следующую команду.

Для косинус-коэффициентов имеем, соответственно, такой результат.
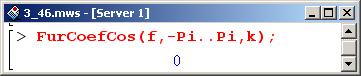
Это и неудивительно – дело в том, что функция нечетная, продолжается (периодически) нечетным образом, поэтому коэффициенты разложения при четных функциях (т.е. косинусах) равны нулю.
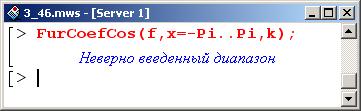
Ниже показано, как процедура реагирует на неверно введенный параметр.
Наконец, определим процедуру, записывающую ряд Фурье для данной функции в символьном виде, т.е. через бесконечную сумму.
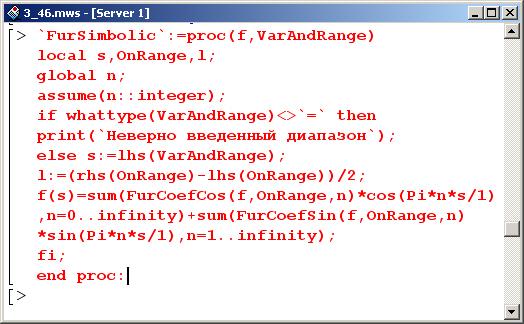
В отличие от процедуры FurSer, в данном случае нет третьего параметра. В процедуре в символьном виде вычисляются коэффициенты разложения (в предположении, что индекс n является целым числом), а сама переменная суммирования n описана как глобальная (поэтому значение ей лучше не присваивать). Результат представляется в виде бесконечной суммы.
