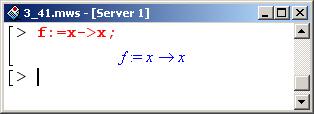
Разложение функций в ряд Фурье
При решении задач математической физики очень часто приходится выполнять разложение по системам ортогональных функций. В тех случаях, когда базовыми являются тригонометрические функции, а само разложение выполняется на конечном интервале, такое разложение называется рядом Фурье.
В приведенном ниже примере для разложения функций в ряд Фурье на интервале создается специальная процедура.
Задача 3.10
Разложить в ряд Фурье приведенные далее функции.
Определим процедуру с такими параметрами: раскладываемая в ряд функция (f), равенство, определяющее переменную и интервал разложения (VarAndRange), а также количество членов ряда (n).
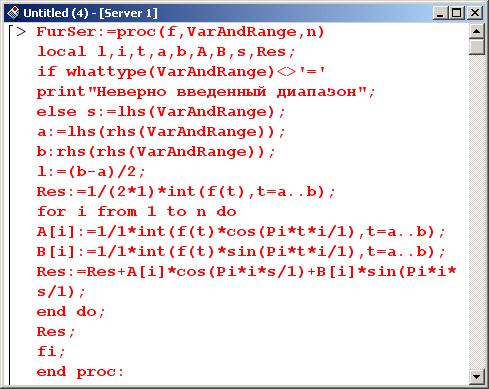
В самом начале процедуры выполняется проверка второго параметра на предмет соответствия типов. Тип аргумента возвращается функцией whattype(), и если он не является равенством выводится сообщение "Неверно введенный диапазон".
В противном случае локальной переменной s в качестве значения присваивается имя переменной, расположенной в левой части равенства VarAndRange. Переменной а присваивается начальная точка диапазона, на котором раскладывается в ряд функция, а переменной b – конечная точка этого диапазона.
Переменная 1 равна половине длины интервала, а начальное значение переменной Res принимается равным нулевому слагаемому косинус-разложения Фурье (т.е. разложения функции по косинусам). Далее в рамках оператора цикла коэффициенты разложения вычисляются, умножаются, соответственно, на косинусы и синусы и прибавляются к переменной Res. По окончании цикла эта переменная возвращается в качестве результата.
Теперь воспользуемся описанной процедурой для разложения в ряд Фурье функций. В частности, определим следующую функцию.