Разложение функций в ряды Тейлора и Лорана
Разложение функции в ряд Тейлора, или, в более общем случае, Лорана, находит самое широкое применение как при решении задач высшей математики, так и в прикладных областях.
В Maple на этот случай предусмотрены такие процедуры:
- taylor() – разложение в ряд Тейлора,
- mtaylor() – разложение в ряд Тейлора функции нескольких переменных,
- series() – обобщенный ряд (для аналитических функций такой ряд совпадает с рядом Тейлора).
На заметку
На этом набор утилит Maple для выполнения разложений в ряды далеко не исчерпывается; их изучение оставляем читателю в качестве самостоятельного задания.
Задача 3.6
Разложить в ряд Тейлора до члена с х функцию: (1+x+x^2)/(1-x+x^2).
Воспользуемся процедурой taylor(), указав первым параметром раскладываемую в ряд функцию, вторым параметром – равенство, определяющее переменную и точку, в окрестности которой выполняется разложение в ряд, а третьим необязательным параметром – порядок "остатка" ряда. Так, если раскладывать функцию следует до слагаемых со степенью 4 включительно, то порядок остатка ряда равен 5.

Определим выражение f, задающее исходную функцию.
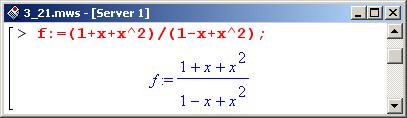
Основную часть ряда обозначим через fl (переменная среды %% ссылается на результат выполнения предпоследней операции (т.е. на ряд для функции), а опция polynom является инструкцией, что указанное первым параметром выражение следует привести к полиномиальному виду).

Теперь можно сравнить, насколько отличаются исходная функция и ее приближение рядом Тейлора (приближение, поскольку остаток ряда был отброшен).
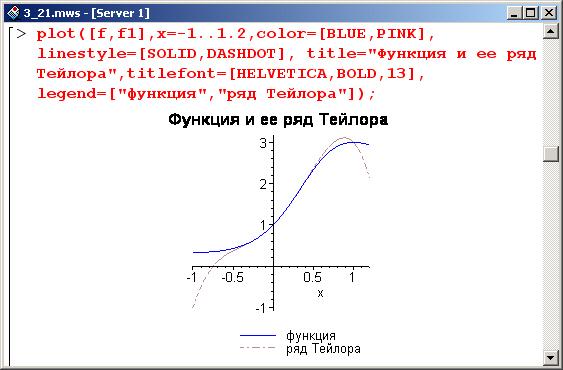
Видим, что даже разложения до четвертой степени достаточно, чтобы корректно аппроксимировать функцию в окрестности нуля. Различие заметно только при существенном удалении от точки разложения.
В следующем примере исследуем вопрос о том, насколько количество оставляемых при разложении функции в ряд слагаемых влияет на точность аппроксимации.
