Исследование рядов на сходимость
Задача 3.4
Исследовать на сходимость ряды: n^5/(2^n+3^n) и ((n-1)/(n+1))^(n*(n-1)).
Сразу определяем процедуру, которая будет "тестировать" ряды. В процедуре сначала проверяется необходимое условие сходимости ряда. Если условие не выполняется, выводится сообщение "Ряд расходится; а(n) не стремится к 0". Если условие выполнено, ряд исследуется на сходимость согласно признаку Коши.
При этом, если вычисляемый предел равен 1 (в такой ситуации признак Коши не позволяет сделать заключение о сходимости ряда), пользователь увидит сообщение: "Необходимо дополнительное исследование".
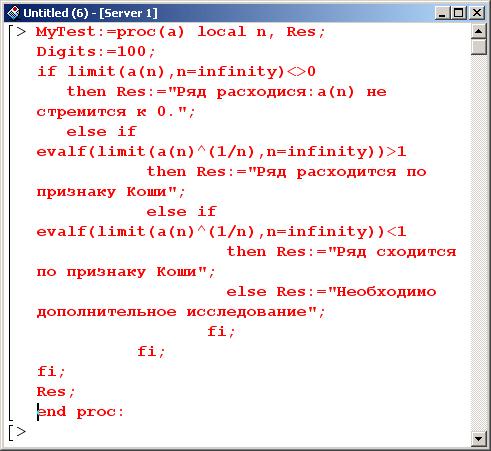
Аргументом процедуры является общий член ряда (это оператор, т.е. а(n) является функцией n). В теле процедуры используется две локальные переменные: n – для "технических" нужд и Res – для записи результата. При этом переменной среды Digits присвоено значение 100 (по умолчанию равно 10) – переменная определяет, сколько значащих цифр будет вычисляться при работе с числами с плавающей точкой.
Внимание!
Приведенная выше процедура определена без учета многих исключительных ситуаций. Например, если Maple не сможет вычислить предел (для этого, правда, выражение должно быть исключительно запутанным), к которому стремится общий член ряда, результат такого неудачного расчета будет представлен в символьном виде и, естественно, не будет равен нулю. В результате появится сообщение о том, что ряд расходится, поскольку общий член в пределе не стремится к нулю – хотя этого на самом деле может и не быть! Такие особенности следует иметь в виду. В частности, чтобы избежать описанной выше неприятности, можно добавить в процедуру оператор проверки типа сравниваемого с нулем выражения.
Теперь с помощью описанной процедуры можно исследовать на сходимость ряды. Стоит обратить внимание на то, как ниже в качестве параметра процедуры указана зависимость общего члена ряда от индекса суммирования.

Еще один способ вызова процедуры состоит в предварительном описании общего члена ряда в виде оператора действия на индекс суммирования.

Ряд сходится по признаку Коши.
Рассмотрим еще один пример.

В следующей задаче используются признаки Даламбера и Раабе.
