Разложение функций в ряды Тейлора и Лорана
Задача 3.7
Разложить в ряд Тейлора функцию.
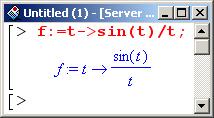
При разложении этой функции в ряд Тейлора порядок остатка указывать не будем.

В подобных ситуациях порядок остатка определяется переменной среды Order; по умолчанию значение этой переменной равно 6. Поэтому в предыдущем выражении последним слагаемым должно было бы быть слагаемое степени 5 по х (соответственно остаток – степени 6). Однако поскольку функция четная, это слагаемое, естественно, отсутствует (точнее, соответствующий коэффициент тождественно равен нулю). Поэтому последним является слагаемое степени 4, а остаток указан как имеющий степень 5 (хотя на самом деле степень остатка равна 6).
Чтобы при вызове процедуры taylor() не указывать, до какой степени проводить разложение, можно изменить значение переменной среды Order.

Определим процедуру F(x,n), которая будет представлять разложение функции f (х) в ряд в окрестности нуля до слагаемых степени порядка n, преобразуя такое разложение в полином.
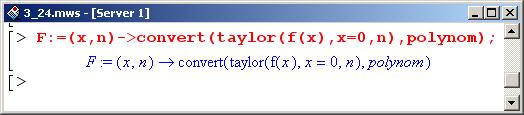
Рассмотрим пример вызова этой процедуры (можно сравнить с результатом разложения, полученным выше).

Теперь построим график исходной функции, ее ряд до степени 5 и ряд до степени 10.
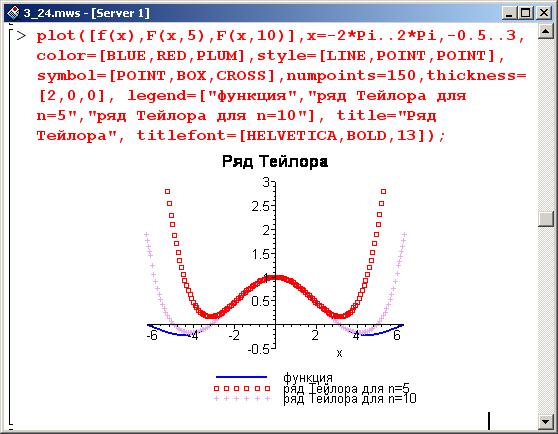
При построении графиков использовалась команда numpoints=150, в которой "частота" базовых точек, по которым строятся графики, увеличивается (по умолчанию – значение 50) в три раза.
Если функция зависит от нескольких переменных, ее также можно разложить в ряд.
