Разложение функций в ряды Тейлора и Лорана
Задача 3.9
Разложить в ряд функцию 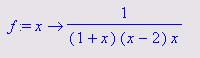 .
.
Как несложно убедиться, функция в точке х=2 имеет особенность. Поэтому использовать процедуру taylor() невозможно. Сначала опишем функцию:

Правила вызова процедуры series () такие же, как и у процедуры taylor().

Видим, что функция f (х) в точке х=2 не является аналитической, поскольку в разложении имеется слагаемое с отрицательным показателем степени. Ряд, который получен выше, фактически является рядом Лорана для функции f(x). Интересно сравнить, как отличаются разложения этой функции окрестности различных точек друг от друга и самой функции. С этой целью определим процедуру, зависящую от трех параметров – раскладываемой в ряд функции, равенства, определяющего переменную и точку разложения, также степени остаточного члена.
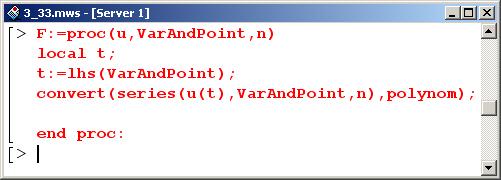
Предполагается, что второй параметр VarAndPoint является равенством (например, х-2). Локальной переменной t присваивается в качестве значения левая часть этого равенства (в приведенном примере это х). Далее выполняется разложение функции-аргумента в ряд и преобразование в полиномиальный вид.
Например, посредством новой процедуры F() полученный выше ряд Лорана можно сгенерировать следующим образом.

