Специальные функции
Выше уже упоминалось о системах ортогональных функций. Эти функции используются при решении задач математической физики (линейных дифференциальных уравнений второго порядка) и часто упоминаются в литературе как специальные функции. Наиболее простыми среди этих функций являются классические ортогональные полиномы.
Для работы с ортогональными полиномами воспользуемся утилитами пакета orthopoly. Данный пакет позволяет работать с полиномами Гегенбауэра (G), Эрмита (Н), Лагерра (L), Лежандра (Р), а также с полиномами Чебышева первого (Т) и второго (u) рода.
Внимание!
Чтобы работать с ортогональными полиномами, совсем не обязательно подключать пакет orthopoly. В Maple ортогональные полиномы доступны и без подключения пакетов. Однако в этом случае формальная ссылка на ортогональные полиномы имеет отличный от представленного выше синтаксис. В частности, ссылка на полиномы Чебышева выполняется как ChebyshevT (полиномы первого рода), ChebyshevU (полиномы второго рода), на полиномы Гегенбауэра – GegenbauerC, на полиномы Якоби-Лежандра – JacobiP и на полиномы Лагерра – LaguerreL.
Чтобы представить, каковы же из себя полиномы Лежандра, поступим следующим образом.
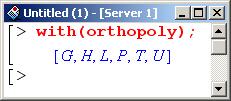
После подключения пакета можно узнать, например, как выглядят первые четыре (начиная с нулевого индекса) полинома.
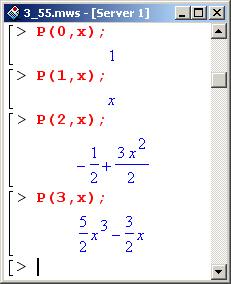
Кроме того, можем проверить, удовлетворяют ли полиномы Лежандра соответствующему уравнению. Для этого прежде опишем процедуру, посредством которой будет формироваться уравнение.

